OBJECTIVE TEST
1.
Correct 0.024561 to three significant figures.
0.03
0.025
0.0245
0.0246
Answer: D
Starting zeros are not significant and so the number of significant digits starts from 24561. The 3 digits lands on 5 but the digit next to it is more than 5 (6) and so 1 is added to the 5 to make it 6.
NOTE
Zeros between other digits are significant. Only starting zeros are insignificant. For instance 3.052306, all the zeros are significant because they are not starting zeros after a decimal point.
2.
A school has a population of 600. Out of this, 120 are girls. What is the probability of meeting a pupil in the school who is a boy?
Answer: D
Probability =
Number of students = 600
Number of boys = 600 - 120 = 480
Probability = =
Note
1. the zeros (0) at the end of 480 and 600 cancel each other
2. 12 divides 48, 4 times and 60, 5 times
3.
In the following diagram, rectangle OABC is enlarged into rectangle OA1B1C1 from center O. OC = 5 cm, OA = 2 cm and AA1 = 1 cm.
Use the diagram to answer the question below.
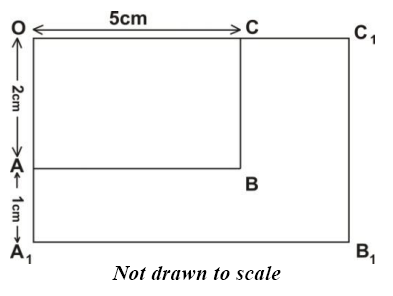
Calculate OC1.
7.5 cm
8 cm
9 cm
12 cm
Answer: A
Scale factor =
Scale factor = = = =
OA1 = A1A + OA = 1 cm + 2 cm = 3 cm
Scale factor = =
OC = 5 cm
=
Cross multiply and solve for OC1
2 x OC1 = 3 x 5
Divide both sides by 2
OC1 =
OC1 =
OC1 = 7.5 cm
4.
An equilateral triangle has side 16cm. A square has the same perimeter as the equilateral triangle. What is the area of the square?
48 cm2
96 cm2
144 cm2
256 cm2
Answer: C
Perimeter is the sum of all the sides of a shape.
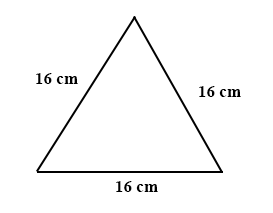
The perimeter of the equilateral triangle = 16 cm + 16 cm + 16 cm = 48 cm
A square has the same perimeter.
Square has 4 equal sides.
Let L = side of the square.
The perimeter of the square = L + L + L + L = 4L
4L = 48
Divide both sides by 4.
L = = 12
The length of the square = 12 cm
Area of a square = Length x Length
Area of the square = 12 cm x 12 cm = 144 cm2
5.
Simplify: (2ab2)2 x 3a3b.
6a4b5
12a3b4
12a6b4
12a5b5
Answer: D
Concepts
1. ax x ay = ax+y, thus if the bases are the same and multiplying, add the powers
2. (axx by)n = ax x n x by x n, thus the outside power multiplies all the powers inside
Applying these two concepts,
(2ab2)2 = 21x2a1x2b2x2 = 22a2b4 = 4a2b4
NOTE: Every number or letter is raised to the power 1, which has no effect, hence 2 = 21 and a = a1
⇒ (2ab2)2 x 3a3b = 4a2b4 x 3a3b
Simplifying the numbers and the ones with the same bases
⇒ 4a2b4 x 3a3b = 4 x 3 x a2xa3b4xb
Applying concept 1,ax x ay = ax+y
⇒ 4 x 3 x a2xa3b4xb = 12a2+3b4+1 = 12a5b5
NOTE: b = b1 ⇒ b4xb = b4xb1 = b4+1 = b5
6.
P = {odd numbers between 20 and 30} and Q = {23, 29}. Which of the following is true?
P ⊂ Q
Q ⊂ P
P = Q
P ∩ Q = Φ
Answer: B
Odd number is a number not divisible by 2.
P = {odd numbers between 20 and 30}
P = {21, 23, 25, 27, 29}
Q = {23, 29}
⊂ stands for subset.
A subset is a set with all its members found in the set it is a subset to.
All the members of Q can be found in P. Hence Q is a subset of P.
7.
Write 2340000 in standard form.
2.34 x 10-6
2.34 x 10-5
2.34 x 106
2.34 x 107
Answer: C
A standard form should be in the form a.bcde x 10n
The decimal point must be after the first non-zero digit.
The n is the number of times the decimal point has to be moved to be right after the first non-zero digit.
If it is moved to the left, the n is positive and if to the right, n is negative.
Every whole number has .0 at the end which is not written.
2340000 = 2340000.0
2340000 = 2.⌒3⌒4⌒0⌒0⌒0⌒0.0 = 2.34 x 106
Note: The power is positive 6 because we had to move the decimal point to the left 6 times.
8.
The gradient of the straight line that passes through points A(3,2) and B(4,8) is
-
-
2
6
Answer: D
Gradient = =
y2 = 8
x2 = 4
y1 = 2
x1 = 3
Gradient =
Gradient =
Gradient = 6
9.
Make d the subject of the relation n = 2d + 3
d =
d =
d =
d =
Answer: C
n = 2d + 3
n - 3 = 2d
Divide both sides of the equation by 2
= d
d =
10.
Kwame, Atsu and Kojo shared a profit of ₵500,000.00 in the ratio 1 : 4 : 3 respectively. How much did Atsu get?
₵62,500.00
₵125,000.00
₵187,500.00
₵250,000.00
₵312,500.00
Answer: D
Respectively means the ratios are in the order of the names mentioned.
The sum of the ratios represents the total amount shared.
Sum of ratios = 1 + 4 + 3 = 8
Atsu's ratio is 4
If 8 = ₵500000
4 = = = ₵250,000
Note:
1. 4 divides itself 1 time and 8, 2 times
2. 2 divides itself 1 time and 50, 25 times
11.
Find the volume of a cylinder of height 3 cm and radius 2 cm.
6π cm3
12π cm3
18π cm3
24π cm3
Answer: B
Volume of a cylinder = πr2h
r2 = r x r
Radius = 2 cm
Height = 3 cm
Volume of a cylinder = π x 2 cm x 2 cm x 3 cm
Volume of a cylinder = π x 12 cm3
Volume of a cylinder = 12π cm3
12.
If the average of 5,6,7 and x is 8, find the value of x
12
14
16
24
Answer: B
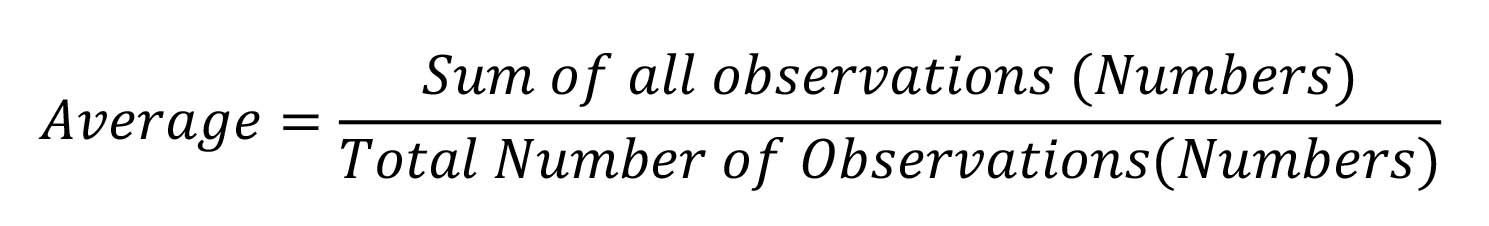
Sum of observations (numbers) = 5+6+7+x
Total number of observations (numbers) = how many numbers are in the observation. In this case 4, thus (5,6,7 and x)
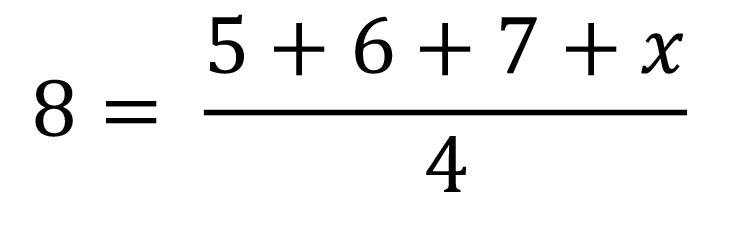
Every number is divisible by 1
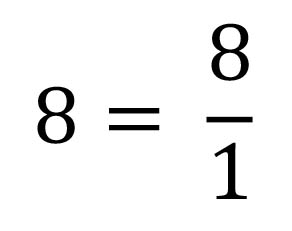
Re-write the equation
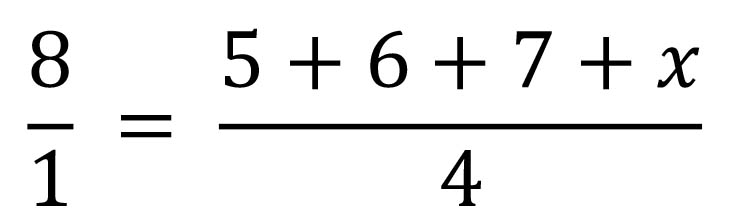
Simplify like terms and cross multiply to solve for the value of x
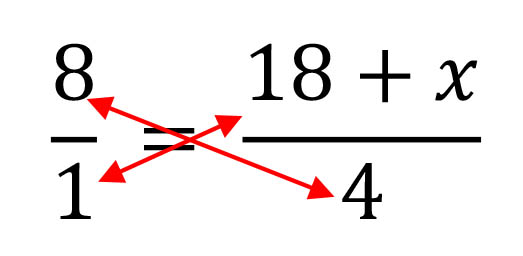
1 x (18+x) = 4 x 8
1 times any number is the same number, hence 1 x (18+x) = 18+x
4 x 8 = 32
18+x = 32
x = 32 - 18
x = 14
13.
If A = {1, 3, 5, 7, 9, 11, 13, 15} and B = {3, 6, 9, 12, 15}, find n(A∩B).
3
5
10
15
Answer: A
Intersection (∩) are elements you can find in both sets.
n in n(A∩B) means the number of elements. So you count how many elements are in A∩B once you are done finding the elements.
A = {1, 3, 5, 7, 9, 11, 13, 15}
B = {3, 6, 9, 12, 15}
As you can see 3, 9 and 15 are the only elements that can be seen in both the sets A and B
Hence A∩B = {3,9,15}
Since you are asked how many elements (n), you count how many elements are in {3,9,15} and I believe you've counted three
Hence n(A∩B) = 3
14.
A pineapple which was bought for GH₵1.00 was sold at GH₵1.30. Calculate the profit percent.
10%
20%
23%
30%
Answer: D
Profit % = x 100
Profit = Selling Price - Cost Price
Profit = 1.3 - 1 = 0.3
Profit % = x 100 = 30%
Note: 0.3 x 100 = 0.⌒3⌒0. = 30
15.
Find the value of m if 4(m + 4) = -8.
-6
-2
2
6
Answer: A
4(m + 4) = -8
Expand the bracket by multiplying each expression in the bracket by 4
4 x m + 4 x 4 = -8
4 x m + 16 = -8
4 x m = -8 - 16
4 x m = -24
Divide both sides of the equation by 4
m = = -6
16.
Simplify + +
Answer: D
+ + =
+ + =
+ + =
17.
Use it to answer the question below.
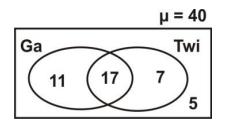
How many pupils speak neither Twi nor Ga?
17
11
7
5
Answer: D
The region outside the two circles represent pupils who don't speak any of the two languages (neither Twi nor Ga)
18.
A match box contains 40 sticks. If 15 of them are spolit, find the probability that a stick chosen at random is not spoilt?
![]()
![]()
![]()
![]()
Answer: C
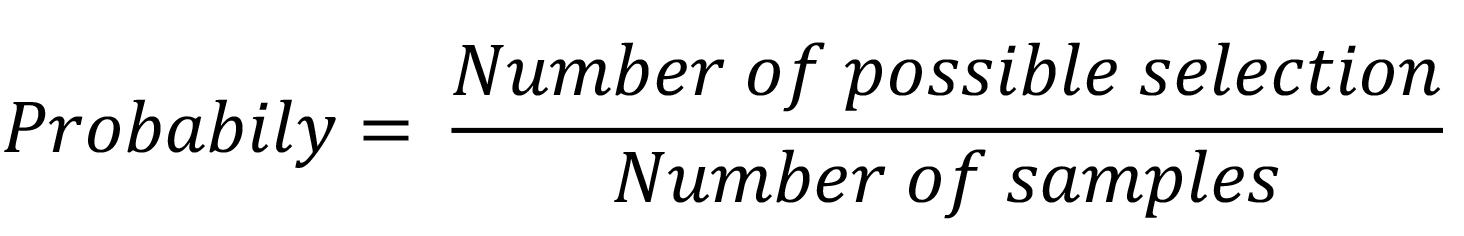
Number of samples = 40
Number of sticks not spoilt = 40 - 15 = 25
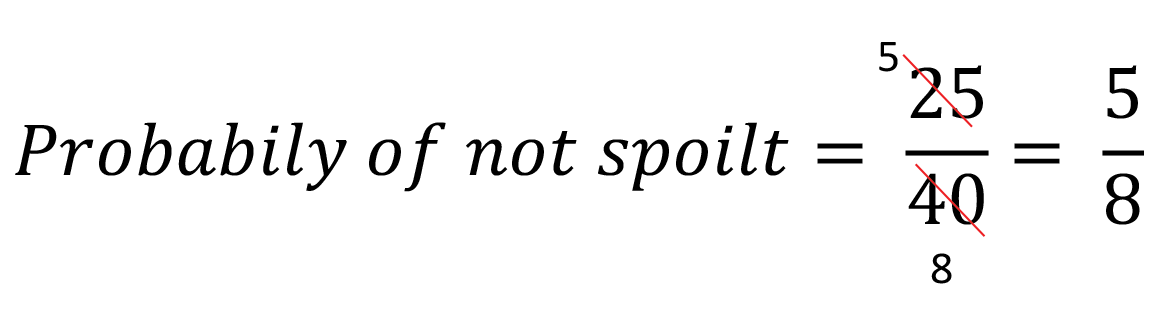
Alternatively
Probability of not = 1 - Probability of is
Probability of is = 1 - Probability of not
Thus when you sum up probability and it's negative, the result should be 1
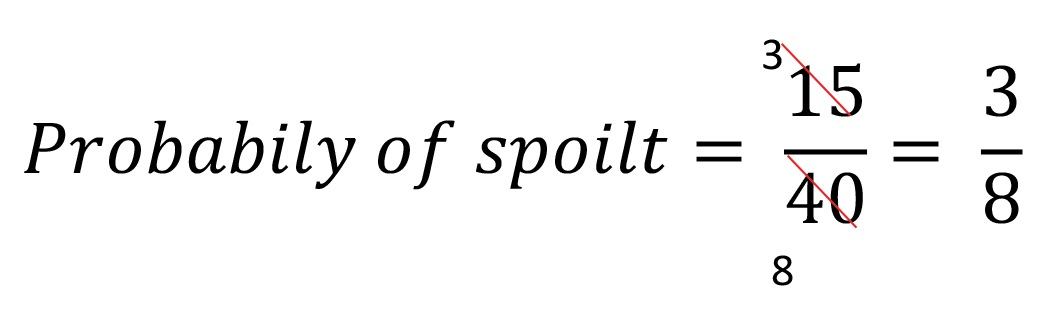
Now we can substract the probability of the spoilt from 1 to get the probability of not spoilt
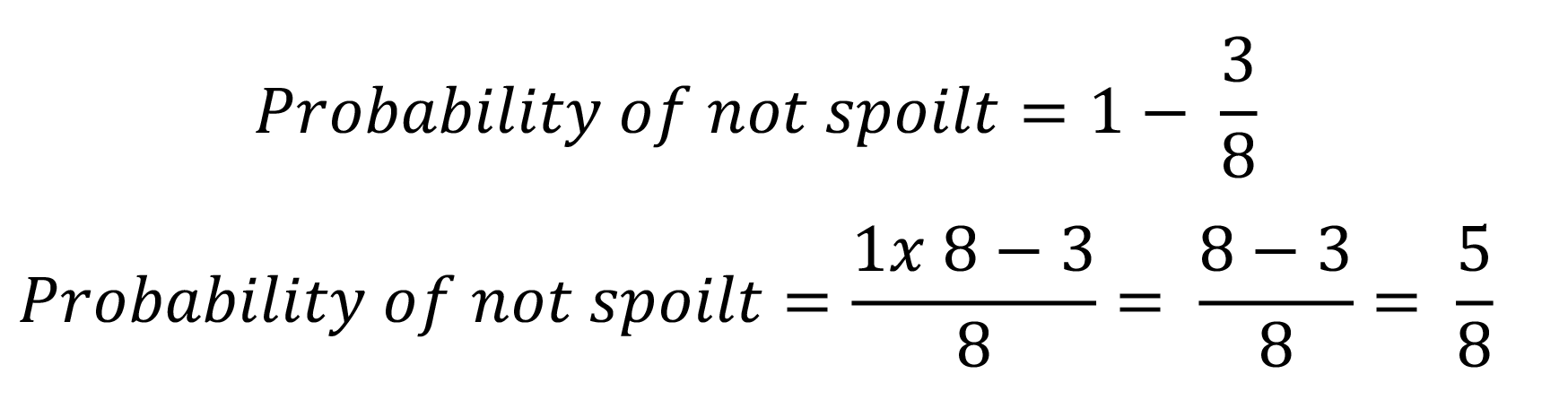
19.
Find k in the vector equation + k = - .
-3
-2
-1
-
2
Answer: B
+ k = -
+ =
+ =
=
The top at the left equals the top at the right and the down at the left equals the down at the right.
3 + 3k = -3
3k = -3 - 3
3k = -6
Divide both sides by 3
k = = -2
Alternatively using the down,
4 + 4k = -4
4k = -4 - 4
4k = -8
Divide both sides by 4
k = = -2
20.
Jane arrived at work at 7:55 a.m and left at 4:15 p.m. For how long was she at work?
7 hr 20 min
7 hr 45 min
8 hr 20 min
8 hr 40 min
Answer: C
7:55 = 7 hours 55 minutes
4:15 = 4 hours 15 minutes
Using the 24 hour system. Afternoon is 12 hours.
4:15 p.m = 12hr + 4hr + 15 min
4:15 p.m = 16hr + 15 min
Hours difference = 16 - 7 = 9 hours
Minutes difference = 15 - 55 = -40 minutes
1 hour = 60 minutes
9 hours = 8 hours + 60 minutes
Total time = 9 hours - 40 minutes
Total time = 8 hours + 60 minutes - 40 minutes
Total time = 8 hours 20 minutes
Total time = 8 hr 20 min
21.
The point (4, 5) is translated to the point (3, 1). What is the translation vector?
Answer: D
Point + Translation vector = Image point
Point = (4, 5) =
Image = (3, 1) =
Let v = Translation vector
+ v =
v = -
v =
v =
22.
Which of the following angles can be constructed by using the arcs at point C in the diagram below?
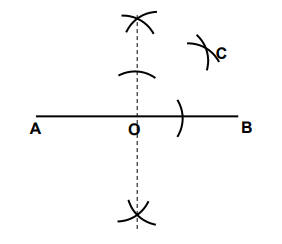
30o
45o
60o
75o
Answer: B
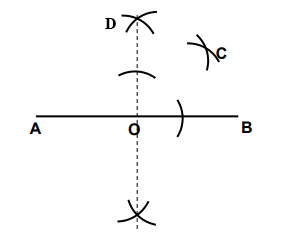
Sum of angles on a straight line is 180o
The arc D bisects the 180o into 2 producing 90o
The arc C also bisects the 90o into 2 producing 45o
23.
Express as a decimal fraction.
0.125
0.375
0.625
0.750
0.875
Answer: C
| 0.625 | |
| 8 |
50
20
40
00 |
24.
Write 356.07 in standard form.
35.607 x 10
35.607 x 102
3.5607 x 102
3.5607 x 10-2
0.35607 x 103
Answer: C
A standard form should be in the form a.bcde x 10n
The decimal point must be after the first non-zero digit.
The n is the number of times the decimal point has to be moved to be right after the first non-zero digit.
If it is moved to the left, the n is positive and if to the right, n is negative.
356.07 = 3.⌒5⌒6.07 = 3.5607 x 102
25.
A rectangular tank is 4 m long, 3 m wide and 2.5 m high. What is the volume of the tank?
24 m3
30 m3
36 m3
48 m3
60 m3
Answer: B
Volume = length x width x height
2.5 =
Volume = 4 m x 3 m x m = 2 m x 3 m x 5 m = 30 m3
Note:
1. 2 divides 4, 2 times and 10, 5 times
2. 5 divides itself 1 time and 25, 5 times
26.
In the diagram below, AB and CD are two intersecting straight lines. Find the value of the angle marked y.
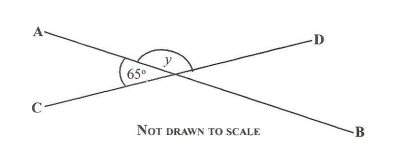
130o
115o
65o
60o
Answer: B
Sum of angles on a straight line is 180
65 + y = 180
y = 180 - 65
y = 115
27.
Kofi had 100 mangoes and sold 80 of them. What is the percentage of mangoes left?
12.5%
18%
20%
25%
Answer: C
Percentage = x 100%
Number of oranges left = 100 - 80 = 20
Total oranges = 100
Percentage = x 100% = 20%
28.
How many faces has a cuboid?
3
4
5
6
Answer: D
Faces of a cuboid
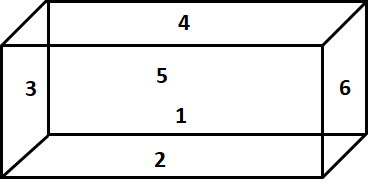
29.
Write 4687.02 in standard form.
46.8702 x 103
46.8702 x 104
4.68702 x 105
4.68702 x 103
0.468702 x 104
Answer: D
A standard form should be in the form a.bcde x 10n
The decimal point must be after the first non-zero digit.
The n is the number of times the decimal point has to be moved to be right after the first non-zero digit.
If it is moved to the left, the n is positive and if to the right, n is negative.
4687.02 = 4.⌒6⌒8⌒7.02 = 4.68702 x 103
30.

Find the set of missing numbers on the number line above.
{-21, -6, 11}
{-21, -10, 11}
{-25, -6, 15}
{-25, -10, 15}
Answer: D
31.
Express 72 as a product of its prime factors.
2 x 33
22 x 32
23 x 3
23 x 32
Answer: D
Prime factors of 72
Prime factors of 72 = 2 x 2 x 2 x 3 x 3 = 23 x 32
32.
Study the triangle of odd numbers and use it to answer the question below.
| 13 | b | c | 19 | |||
| 7 | 9 | a | ||||
| 3 | 5 | |||||
| 1 |
Evaluate: a + b + c
24
29
36
43
Answer: D
Series of odd numbers are obtained by adding 2 to an odd number to get its consecutive odd number.
In the first row, the odd numbers are obtained as follows:
13, 13+2 = 15, 15+2 = 17, 17+2 = 19
b = 15 and c = 17
In the second row, the odd numbers are obtained as follows:
7, 7+2 = 9, 9+2 = 11
a = 11
a + b + c = 11 + 15 + 17 = 43
33.
In a school of 940 pupils, the number of girls exceeds the number of boys by 150. How many girls are there in the school?
620
545
470
395
Answer: B
Let x = number of girls in the school
The number of girls exceeds the number of boys by 150 → number of boys = x - 150
Number of girls + Number of boys = 940
x + x - 150 = 940
2x = 940 + 150
2x = 1090
Divide both sides by 2 to solve for x
x = = 545
There are 545 girls in the school.
1090 divided by 2
| 545 | |
| 2 |
1090
90
00 |
34.
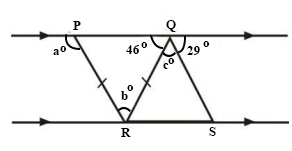
In the diagram above, PQ is parallel to RS and |PR| = |QR|.
Use the diagram to answer the question below.
Find b.
29
46
88
92
105
Answer: C
Triangle PRQ is isosceles triangle. The base angles are the same.
Angle RPQ = Angle RQP = 46°
Angle RPQ + Angle RQP + b = 180°(sum of interior angles of a triangle is 180°)
46° + 46° + b = 180°
92° + b = 180°
b = 180° - 92°
b = 88°
35.
Simplify: -15 - (-20) + (-10).
-45
-5
-25
5
Answer: B
-(-) = -1 x - = +
+(-) = +1 x - = -
-15 - (-20) + (-10) = -15 + 20 - 10
-15 - (-20) + (-10) = -15 - 10 + 20
-15 - (-20) + (-10) = -25 + 20
-15 - (-20) + (-10) = -5
36.
If y : 28 = 5 : 7, find y.
5
20
31.2
37.5
Answer: B
y : 28 = 5 : 7
Change the ratios to fraction format.
=
Cross multiply.
y x 7 = 28 x 5
Divide both sides by 7
y =
Note: 7 divides itself 1 and 28, 4 times.
y = 4 x 5
y = 20
37.
How many lines of symmetry has a square?
0
1
2
3
4
Answer: E
A line of symmetry is the line that divides a shape or an object into two identical parts.
38.
Given that r = and s = , find r - 2s.
Answer: B
Multiplying a vector by a number
c = c x =
Addition of vectors
+ =
Subtraction of vectors
- =
r = and s =
r - 2s = - 2
r - 2s = -
r - 2s = -
r - 2s =
-- = +
r - 2s =
r - 2s =
39.
Find the area of a circle whose diameter is 7 cm.
[Take π = ]
11 cm2
38 cm2
44 cm2
54 cm2
Answer: B
Area of a circle = πr2
Area of a circle = π x r x r
Radius is half of the diameter
Radius =
π =
Area of circle = x x
Note: 2 divides itself once and 22, 11 times and the 7 at the denominator cancels one of the 7s at the numerator
Area of circle = = = 38
40.
Find the Lowest Common Multiple (LCM) of 22 x 3 x 52 and 23 x 32 x 5.
22 x 3 x 5
22 x 32 x 52
23 x 3 x 5
23 x 32 x 52
Answer: D
The Lowest Common Multiple (LCM) is the multiplication of each of the prime factors in their highest powers.
The prime factors are 2, 3 and 5
The highest power for the prime number 2 is 3
The highest power for the prime number 5 is 2
The highest power for the prime number 3 is 2
Lowest Common Multiple (LCM) = 23 x 32 x 52
THEORY QUESTIONS
(a)
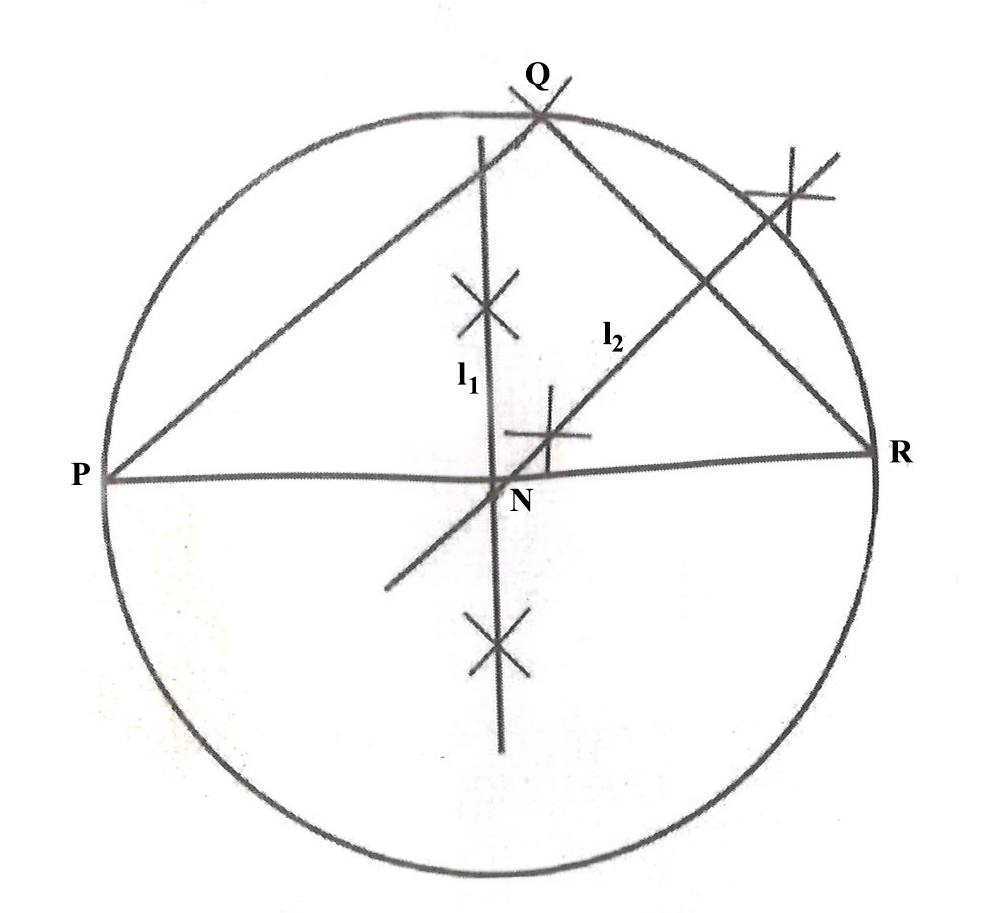
Using a ruler and a pair of compass only:
(i)
construct triangle PQR such that |PR| = 8 cm, |PQ| = 6 cm and |QR| = 5 cm;
(ii)
construct the perpendicular bisector of |PR| and label it l1;
(iii)
construct the perpendicular bisector of |QR| and label it l2;
(iv)
Label the point of intersection of l1 and l2 as N.
(v)
With N as centre and radius equal to draw a circle.
(b)
(i)
Measure the radius of the circle.
(ii)
Calculate the circumference of the circle, correct to 3 significant figures.
[Take π = 3.14]
(a)
(b)
(i)
Radius = 4 cm
(ii)
Circumference = 2πr
π = 3.14
r = 4 cm
Circumference = 2 x 3.14 x 4 cm = 25.12 cm
Circumference = 25.1 cm (3 Significant figures)
(a)
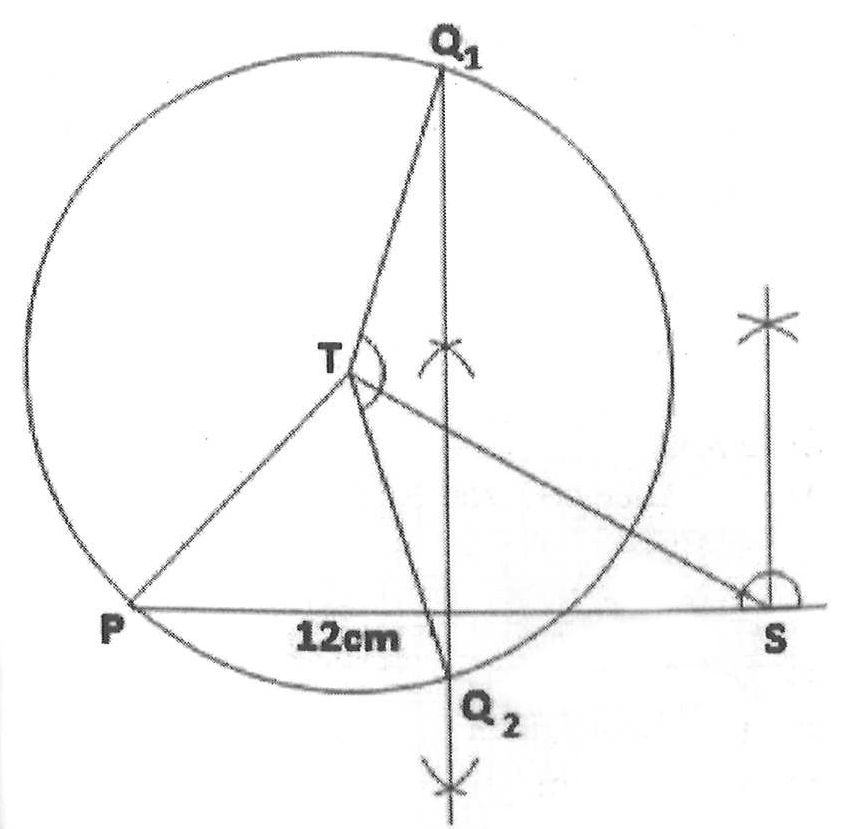
Using a ruler and a pair of compasses only, construct triangle PST with angle PST = 30o, |ST| = 9 cm and |PS| = 12 cm.
(b)
With T as center, draw a circle of radius 6 cm.
(c)
Construct the perpendicular bisector (mediator) of line PS.
(d)
Label the intersections of the circle and the mediator Q1 and Q2.
(e)
(i)
Measure |Q1Q2|.
(ii)
Measure angle Q1TQ2.
(a-d)
(e)
(i)
|Q1Q2| = 11.5 cm
(ii)
∠Q1TQ2 = 145o
(a)
There are 20 students in a hostel. 16 of them are fluent in French and 10 of them are fluent in English. Each student is fluent in at least one of the two languages.
(i)
Illustrate this information on a Venn diagram
(ii)
How many students are fluent in both English and French?
(b)
The sum of the ages of two brothers Kofi and Kweku is 35. Kofi's age is two-thirds of Kweku's age. Find their ages.
(a)
(i)
Let U = {students in the hostel}
n(U) = 20
E = {students who are fluent in English}
n(E) = 10
F = {students who are fluent in French}
n(F) = 16
x = number of students who are fluent in both English and French.
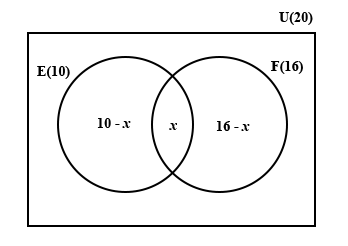
(ii)
10 - x + x + 16 - x = 20
26 - x = 20
26 - 20 = x
6 = x
x = 6
∴ 6 students are fluent in both English and French.
(b)
Sum means addition.
Kofi's age + Kweku's age = 35
Let Kweku's age = x
Kofi's age is two-thirds of Kweku's age
is means equal to
two-third =
Kofi's age = x Kweku's age
Kofi's age = x x = x
Kofi's age + Kweku's age = 35
x + x = 35
Get rid of the fraction by multiplying both sides of the equation by the denominator (3)
3 x x + 3 x x = 35 x 3
2x + 3x = 105
5x = 105
Divide both sides by 5
x = = 21
Kofi's age = x
Kofi's age = x 21 = 2 x 7 = 14
∴ Kweku is 21 years and Kofi is 14 years.
(a)
The volume of a cylinder is 220 cm3. The radius of the cross-section is 2.5 cm. Find the height of the cylinder.
[Take π = ]
(b)
Each of the interior angles of a regular polygon is 140°. How many sides does it have?
(a)
Volume of a cylinder = π x radius x radius x height.
volume = 220
π =
radius = 2.5 =
Let h = the height of the cylinder.
220 = x x x h
220 = x h
Get rid of the fraction by multiplying both sides of the equation by 7 x 10 x 10
220 x 7 x 10 x 10 = 22 x 25 x 25 x h
Divide both sides by 22 x 25 x 25
h =
Cancel out.
Note:
1. 22 divides itself 1 time and 220, 10 times
2. 5 divides 10, 2 times and 25, 5 times
3. 5 divides itself 1 time and 10, 2 times
4. 5 divides 10, 2 times and 25, 5 times
h =
h = = 11.2 cm
(b)
Interior Angle =
Where n = number of sides of the regular polygon.
Interior Angle = 140°
140 =
Get rid of the fraction by multiplying both sides of the equation by the denominator (n).
140 x n = (n - 2) x 180
140n = 180n - 360
360 = 180n - 140n
360 = 40n
Divide both sides by 40
n =
n = 9
∴ the regular polygon has 9 sides.
(a)
(i)
Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes OX and OY on a graph sheet.
(ii)
Mark on the same graph sheet, the x-axis from -5 to 5 and y-axis from -6 to 6.
(iii)
Plot the points A(2, 5), B(2, 2) and C(4, 2). Join the points A, B and C to form triangle ABC.
(iv)
Using the y as mirror line, draw the image triangle A1B1C1 of the triangle ABC such that A → A1, B → B1 and C → C1. Write down the coordinates of A1, B1 and C1.
(v)
Draw the image triangle A2B2C2 of triangle ABC under anticlockwise rotation of 180° about the origin where A → A2, B → B2 and C → C2. Write down the coordinates of A2, B2 and C2.
(b)
Given that a = , b = and c = , evaluate 2a - 3c + b.
(a)
(i - iii)
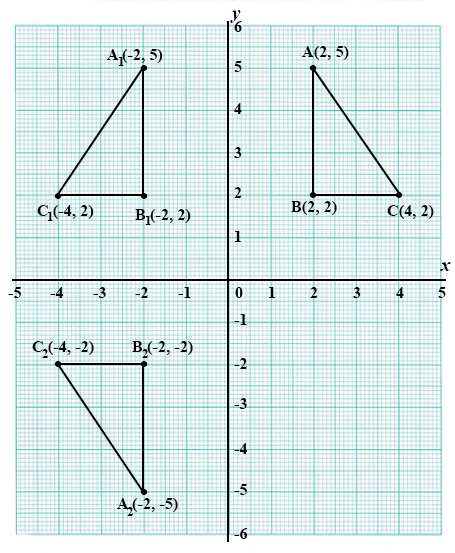
(iv)
y-axis as mirror/reflection in y-asis
→
Thus the x is negated.
A → A1
A(2, 5) → A1(-2, 5)
B → B1
B(2, 2) → B1(-2, 2)
C → C1
C(4, 2) → C1(-4, 2)
(v)
180° Anticlockwise rotation
→
Thus the both the x and y are negated.
A → A2
A(2, 5) → A2(-2, -5)
B → B2
B(2, 2) → B2(-2, -2)
C → C2
C(4, 2) → C2(-4, -2)
(b)
a = , b = and c =
2a - 3c + b = 2 - 3 +
2a - 3c + b = - +
2a - 3c + b = - +
2a - 3c + b =
- (-) = - - = +
2a - 3c + b =
2a - 3c + b =
A landlady rented out her house for ₵240,000.00 for one year. During the year she paid 15% of the rent as income tax. She also paid 25% of the rent as property tax and spent ₵10,000.00 on repairs.
Calculate:
(a)
The landlady's total expenses.
(b)
The remainder of the rent after the landlady's expenses.
(c)
The percentage of the rent she spent on repairs.
(a)
Total expenses = Income tax + Property tax + Repairs
% means over 100
of means multiplication (x)
She paid 15% of the rent as income tax
Income tax = x ₵240000 = 15 x ₵2400 = ₵36,000
Note: the zeros (0) at the end of 240000 and 100 cancel each other
She paid 25% of the rent as property tax
Property tax = x ₵240000 = 25 x ₵2400 = ₵60,000
Repairs = ₵10,000
Total expenses = ₵36,000 + ₵60,000 + ₵10,000
Total expenses = ₵106,000.00
(b)
Remainder of the rent = Rent - Total Expenses
Remainder of the rent = ₵240000 - ₵106,000
Remainder of the rent = ₵134,000.00
(c)
Percentage = x 100%
Percentage of rent on repairs = x 100%
Percentage of rent on repair = x 100%
Note:
1. the zeros (0) at the end of 10000 and 240000 cancel each other
2. 4 divides 24, 6 times and 100, 25 times
Percentage of rent on repair = = 4.167%