1.
Expand (2a + b) (a + 2b)
2a2 + 2b2
2a2 + b2
5a2 + 2a2
2a2 + 2a + 4ab2
2a2 + 5ab + 2b2
2.
Find the missing number in the following binary operation:
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | |
| - | * | * | * | * | * | * | * |
| 1 | 1 | 1 | 0 | 1 | 1 |
111011
101001
100011
101110
101011
3.
If x = {1, 3, 5, 7, 9, 11, 13, 15}, find the truth set of x – 3 ≥ 10.
{15}
{13,15}
{11,13,15}
{9,11,13,15}
{7,9,11,13,15}
4.
Which of these has the least number of lines of symmetry?
An equilateral triangle
A rectangle
A square
A circle
An isosceles triangle
5.
Find 2% of ₵2,000.00
₵40.00
₵50.00
₵100.00
₵800.00
₵5,000.00
6.
Find the highest common factor of 18, 36 and 120.
22 × 33 × 5
2 × 3 × 5
2 × 3
23 × 22
32 × 22
7.
Arrange the fractions , , in ascending order.
, ,
, ,
, ,
, ,
, ,
8.
Make b the subject of the relation = + c
b =
b =
b =
b =
b =
9.
A man has three children whose ages are 9 years, 12 years and 24 years. Find the ratio of their ages.
1 : 2 : 3
1 : 2 : 4
2 : 3 : 6
3 : 4 : 8
3 : 6 : 8
10.
Ten students in Kwamekrom JSS took 9 days to weed the school compound. How long would 15 students take to weed the compound if they worked at the same rate?
5 days
6 days
13 days
14 days
16 days
11.
Which of the following inequalities is / are true?
I: > II: > III: > .
I only
II only
III only
I and II only
I and III only
12.
Find the image of P in the mapping below:
| 1 | 2 | 3 | P |
| ↓ | ↓ | ↓ | ↓ |
| 3 | 5 | 7 | ? |
A
P2 + 2
P2 + 1
2P + 1
P + 2
P2 - 2
13.
A car travelled a distance of 50 km in an hour. What distance did it travel in 30 minutes at the same speed?
1,500 km
100 km
80 km
25 km
20 km
14.
In an enlargement, the area of the object was multiplied by 144 to get the area of the image. Find the scale factor of the enlargement.
12
36
48
72
144
15.
Mr. Yevu saved ₵2,500.00 at a simple interest rate of 25% per annum for 4 years. Calculate the interest he earned on his savings.
₵625.00
₵2,500.00
₵3,125.00
₵5,000.00
₵10,000.00
16.
The table below gives the number of goals scored by a football team in a league season:
| Number of goals scored in a match | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 1 | 7 | 6 | 4 | 1 | 1 |
Use it to answer the question below.
Find the total number of goals scored by the team.
41
40
20
19
15
17.
The table below gives the number of goals scored by a football team in a league season:
| Number of goals scored in a match | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 1 | 7 | 6 | 4 | 1 | 1 |
Use it to answer the question below.
What is the mean number of goals scored by the team?
7
6
4
2
1
18.
The table below gives the number of goals scored by a football team in a league season:
| Number of goals scored in a match | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 1 | 7 | 6 | 4 | 1 | 1 |
Use it to answer the question below.
What is the total number of matches played in the league season?
6
7
19
20
40
19.
The probability of obtaining a head when a coin is tossed is . What is the probability of obtaining a tail?
1
0
20.
Given that a = and b = , find a + 2b.
21.
Find in base ten the value of 4 in 143five.
48
40
25
20
9
22.
If the interior angle of a regular polygon is 120°, how many sides does it have?
5
6
7
8
9
23.
Simplify
6
7
7
10
14
25.
Find the solution set of n - > - n.
{n:n > -1}
{n:n = 0}
{n:n > }
{n:n > }
{n:n > 1}
25.
In the diagram below, |AE| = |ED| = |DC| = |CE|.
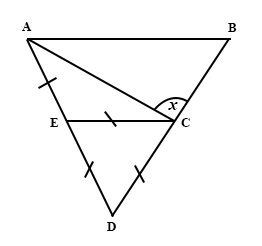
Calculate the size of the angle marked x.
150°
120°
90°
60°
30°
26.
Five times a number is four more than the number. Find the number.
1
-1
27.
A basket contains 450 oranges, if each orange costs ₵15.00, find the total cost of the oranges.
₵30.00
₵465.00
₵435.00
₵675.00
₵6,750.00
28.
A bottle of soft drink costs ₵200.00. The commission paid on one bottle is 2% of the cost price. Find the commission paid on 24 bottles of the soft drink.
₵96.00
₵296.00
₵400.00
₵4,704.00
₵4,800.00
29.
If is equivalent to , find the value of x.
1
2
4
5
6
30.
Write 39.975 km correct to three significant figures.
39 km
39.975
49 km
40.0 km
40.9 km
31.
Find x, if + = 1
-
-
32.
The bearing of Aboku from Bebeka is 055°. What is the bearing of Bebeka from Aboku?
035°
055°
125
235°
305°
33.
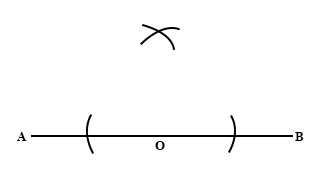
The diagram above shows the construction of :
the perpendicular bisector of the line
an angle of 45° at the point A
an angle of 45° at the point B
an angle of 90° at the point O
an angle of 90° at the point B
34.
The dimensions of the rectangle are given in base two. Find its perimeter.
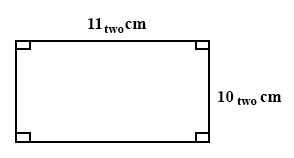
100two cm
101two cm
110two cm
1001two cm
1010two cm
35.
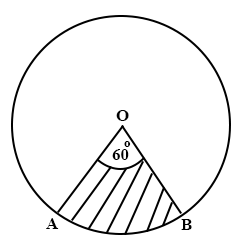
The area of circle, centre O, is 120 cm2. Angle AOB is 60°. Find the area of sector AOB.
2 cm2
3 cm2
6 cm2
20 cm2
60 cm2
36.
In the diagram, ABCD is a parallelogram; BC and AF are straight lines. Angle ABC = 110° and angle DEF = 40°. Find the angle marked θ.
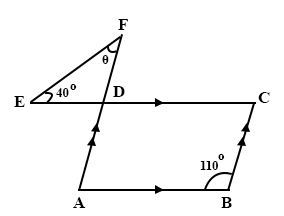
30°
40°
50°
70°
110°
37.
In the diagram below AC // DF. Angle CBT is 40° and angle DET is 140°
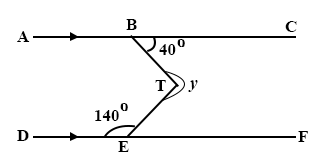
320°
280°
220°
100°
80°
38.
In the diagram below, the angle of elevation of K from M is
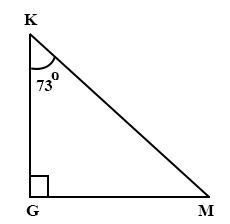
17°
73°
90°
107°
163°
39.
In the diagram below, ACD is an isosceles triangle in which |AD| = |AC| and DC is parallel to BE, find the value of the angle marked x.
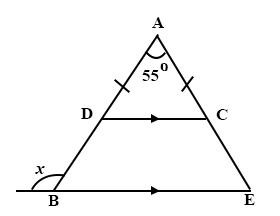
55°
62.5°
110°
117.5°
125°
40.
Three girls Ama, Adjoa and Abena measured the length of the sides of 3 right-angled triangles as follows:
Ama's measurements were 80 mm, 40 mm, 50 mm.
Adjoa's measurements were 50 mm, 120 mm, 130 mm.
Abena's measurements were 20 mm, 30 mm and 40 mm.
Whose measurement(s) was / were correct?
Ama's only
Abena's and Ama's
Adjoa's and Abena's
Ama's and Adjoa's only
Adjoa's only
(a)
Simplify -
(b)
Solve 5(a – 5) – (2a + 6) = 4
(c)
If r = and q = , calculate 6(r + 2q).
Using a ruler and a pair of compasses only,
(a)
construct a triangle ABC such that |BA| = 10 cm, angle ABC = 90° and angle BAC = 30°. Measure the length BC.
(b)
(i)
Bisect the angle ACB to meet BA at D.
(ii)
What type of triangle is CDA?
(c)
Calculate the area of triangle ABC
Olu bought a radio for ₵65,000.00. After one year the radio was valued at 75% of the cost price.
(a)
What was the price of the radio after one year?
(b)
If he sold the radio for ₵55,700.00, calculate his profit or loss over the cost price.
(a)
Using a scale of 2 cm to 1unit on both axes, draw two perpendicular lines OX and OY on a graph sheet.
(b)
On this graph sheet, mark the x-axis from –5 to 5 and the y-axis from –6 to 6.
(c)
Plot on the same graph sheet the points A(-2, 4) and B(4, -5). Join the points A and B with the help of a ruler.
(d)
Using the graph , find
(i)
the gradient (slope) of the line AB;
(ii)
the value of x, when y = 0;
(iii)
the value of y when x = 2
(e)
Plot on the same graph sheet the points C(-3, -1) and D(3, 3). Join the points C and D. with the help of a protractor, measure the angle between the lines AB and CD. What is the gradient of the line CD?
The ages of 20 school children were recorded as follows:
| 13 | 9 | 15 | 17 | 13 |
| 9 | 11 | 9 | 11 | 15 |
| 17 | 15 | 11 | 9 | 9 |
| 11 | 15 | 11 | 11 | 11 |
(a)
Make a frequency table for the data using the ages of 9, 11, 13, ..........
(b)
Use your table to calculate the mean age (correct to the nearest whole number).