1.
P = {prime numbers less than 20} and Q = {odd numbers less than 10}.
Find P ∩ Q
{2, 3}
{1, 3, 5, 7, 11)
{3, 5, 7, 9}
{3, 5, 7}
{3, 5, 7, 11}
2.
Convert 104ten to a binary numeral.
1101000
1010100
1101100
1011010
1110100
3.
What is the H.C.F of 48, 30 and 18?
2
3
5
6
9
4.
Express 34m 5cm 6mm in millimetres
340506 mm
342506 mm
34056 mm
30456 mm
34565 mm
5.
Write 356.07 in standard form.
35.607 x 10
35.607 x 102
3.5607 x 102
3.5607 x 10-2
0.35607 x 103
6.
Divide by
1
1
1
3
7.
Which property is illustrated by the statement a × (b + c) = a × b + a × c?
Inverse
Identity
Commutative
Distributive
Associative
8.
How many edges has a cube?
4
6
8
12
18
9.
What is the mode of the following numbers: 4, 5, 3, 3, 4, 2, 7, 6, 5, 4, 4, 1?
3
4
5
6
7
10.
What is the rule for the mapping below?
| x | 1 | 2 | 3 | 4 | 5 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| y | 2 | 4 | 8 | 16 | 32 |
y = 2x + 2
y = 2x
y = x + 2
y = x + 1
y = 2x
11.
Solve 4x – 6 < -2
x < 1
x > 1
x < -1
x > -1
x < 4
12.
In a school, 80 pupils wrote an examination and 64 of them passed. What is the percentage of pupils who passed?
8%
16%
20%
64%
80%
13.
The interior angle of a regular polygon is 120°. How many sides has the polygon?
3
4
5
6
8
14.
Kofi throws a die. What is the probability that he throws the number 2?
1
15.
What is the image of -4 under the mapping x → x - 2?
4
2
0
–2
–4
16.
Find the value of p in the diagram below.
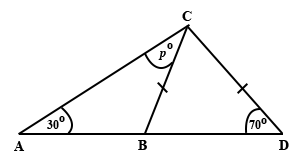
110
90
70
50
40
17.
Make a subject of the relation P = 2(a + b)
a =
a =
a =
a =
a =
18.
What is the value of x in the relation 5x = 125?
2
3
4
5
6
19.
Calculate the length of QR in triangle PQR
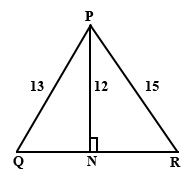
11
14
16
17
25
20.
Five cards are numbered one to five. A card is picked at random. What is the probability that it has an even number?
1
21.
If u = and v = , find 3u + 2v.
22.
Arrange the following fractions in descending order , , ,
, , ,
, , ,
, , ,
, , ,
, , ,
23.
How many lines of symmetry has a square?
0
1
2
3
4
24.
If (x, y) → (x, 2y), find the image of (2, - )
(2, -2)
(2, -)
(2, -2)
(2, -)
(2, 2)
25.
The ages in years of eight boys are: 14, 14.5, 15, 12, 11.5, 13, 10.5, 13.5.
What is their average age?
14
13
12
11
10
26.
Convert 133five to a base ten numeral.
23
25
31
40
43
27.
Find the simple interest on ₵15,000.00 at rate of 20% per annum for 5 years.
₵10,000.00
₵15,000.00
₵30,000.00
₵50,000.00
₵90,000.00
28.
List all members of the set {x: 2 < x < 8, x is an integer}
{3, 4, 5}
{2, 3, 4, 5, 6, 7, 8}
{2, 2, 3, 4, 5, 6, 7, 8}
{3, 3, 3, 4, 5, 6, 7, 8}
{3, 4, 5, 6, 7}
29.
Simplify 348.94 - 188.34
60.60
60.68
160.60
200.60
206.60
30.
Find the difference between the values of (2d)2 and 2d2 when d = 3
16
18
24
28
54
31.
The heights of two boys are in the ratio 4 : 5. The shorter boy is 80 cm. What is the height of the taller boy?
100 cm
150 cm
164 cm
180 cm
200 cm
32.
Factorize completely 5xy + 10ny
5y(x + n)
5y(x + 2n)
5xy(1 + 2n)
5(xy + 2ny)
x(5x + 10n)
33.
If 13x – 12 = 5x + 60, find x
–9
–6
4
6
9
34.
The length of a spring when a mass of n kg is hung on it is L = (74 + 15n) mm. What is the length of the spring when a mass of 1.20kg is hanged on it?
75.20 mm
89.00 mm
92.00 mm
97.00 mm
104.00 mm
35.
In the figure below, triangle ABC is an enlargement of triangle ADE. If |AE| = 20 cm and |EC| = 10 cm. What is the scale factor of the enlargement?
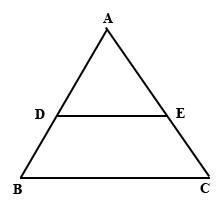
2
3
36.
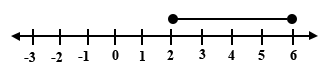
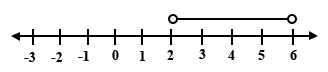
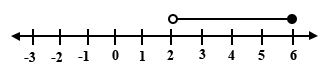
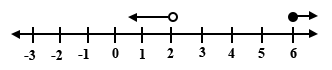
Which of the number lines below represents the inequality 2 < x ≤ 6?
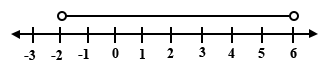
37.
A cylinder has a radius 6 cm and height 7 cm. Find its volume.
[Take π = ]
132 cm3
264 cm3
294 cm3
792 cm3
924 cm3
38.
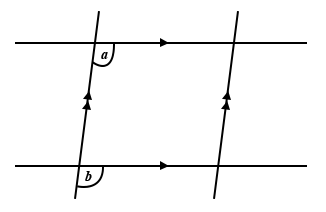
The angles a and b in the figure above are
interior opposite
corresponding
vertically opposite
acute
alternate
39.
A man travelled a distance of 1.2 km in 30 minutes. What distance can he cover in 55 minutes travelling at the same speed?
1.375 km
2.02 km
2.2 km
12.02 km
13.25 km
40.
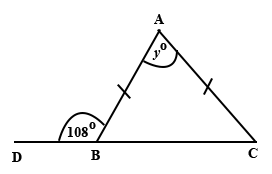
In the diagram above, ∆ABC is an isosceles triangle. ∠ABD is 108°. Find the value of y.
72
60
48
36
24
(a)
There are 20 students in a hostel. 16 of them are fluent in French and 10 of them are fluent in English. Each student is fluent in at least one of the two languages.
(i)
Illustrate this information on a Venn diagram
(ii)
How many students are fluent in both English and French?
(b)
The sum of the ages of two brothers Kofi and Kweku is 35. Kofi's age is two-thirds of Kweku's age. Find their ages.
(a)
Using a ruler and a pair of compasses only
(i)
construct triangle ABC such that |AB| = 9 cm, angle BAC = 60° and angle ABC = 45°.
(ii)
construct a line from the point C perpendicular to line AB and let it meet AB at P. Measure |CP| and |AP|
(b)
What is the value of angle ACP?
(a)
Mansah earns a salary of ₵10,000.00 per month as a sales girl. In addition to the salary, she is given a commission of 1.5% of whatever sales she makes in a month. In January this year, she made sales of ₵7,500,000.00. What was the total amount Mansah earned at the end of January?
(b)
The diagram below shows a circle with centre O and radius 14 cm. The shaded region AOB is a sector with angle AOB = 72°.
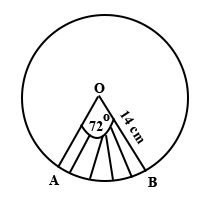
Find:
(i)
The length of the minor arc AB
(ii)
The area of the shaded sector AOB
[Take π = ]
(a)
Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes, OX and OY on a graph sheet.
(b)
On the graph sheet, mark the x-axis from –5 to 5 and the y-axis from –6 to 6
(c)
(i)
Plot on the same graph sheet the points A(1, 1), B(4, 1), C(1, 4).
(ii)
Join the points to form a triangle. What type of triangle have you drawn?
(d)
Draw the image triangle A1B1C1 of ABC under a reflection in the y-axis, where A→A1, B→B1 and C→C1. Label the vertices and the co-ordinates clearly.
(e)
Draw the image triangle A2B2C2 of triangle ABC under an enlargement with scale factor –1 with the centre of enlargement as the origin (0,0), where A→A2, B→B2 and C→C2. Show all lines of enlargement. Label the vertices and co-ordinates clearly
(f)
What single transformation maps A1B1C1 onto A2B2C2 where A1→A2, B1→ B2 and C1→C2?
(a)
The data below shows the distribution of the ages of workers in a factory.
| Ages (in years) | No. of workers |
| 19 | 3 |
| 24 | 7 |
| 29 | 8 |
| 34 | 4 |
| 39 | 5 |
| 44 | 3 |
(i)
How many workers are there in the factory?
(ii)
What is the modal age of the distribution?
(iii)
Calculate the mean age of the workers, correct to one decimal place.
(b)
(i)
Make T the subject of the relation
I =
(ii)
If I = ₵40,000.00, P = ₵64,000.00 and R = 25%, find the value of T in years.