1.
Two sets which have no common members are known as ......
equal sets
equivalent sets
empty sets
disjoint sets
union
2.
P = {0, 2, 4, 6} and Q = {1, 2, 4, 5}. Find P ∩ Q.
{0, 6}
{2, 4}
{0, 4}
{0, 2, 6}
{0, 1, 2, 4, 5}
3.
Evaluate [(4 – 1) – (5 – 6)]
–4.0
1.0
2.0
3.0
4.0
4.
Find the highest(greatest) common factor of 35 and 70.
5
7
10
35
70
5.
Write 1101101two in base ten
31
43
108
109
218
6.
State the property used in the statement: p(q + r) = pq + pr
Associative
Commutative
Distributive
Identity
Universal
7.
If n2 + 1 = 50, find n
7
24.5
25
49
8.
Evaluate
0.0049
0.049
0.49
4.9
49
9.
In the relation = + , if R1 = 1 and R2 = 3,
find R
10.
Arrange the following from the highest to the lowest: , -9, and 0.
-9, ,
-9, 0, ,
, , 0, -9
, , -9, 0
, , 0, -9
11.
The total numbers of goals scored each month by a football team are:
3, 4, 8, 2, 4, 6, 4, 8, 7 and 6.
What is the mode?
2
4
5
6
8
12.
A trader sold 90 oranges at 3 for ₵50.00. How much did she get from selling all the oranges?
₵1,500.00
₵4,500.00
₵6,000.00
₵15,000.00
₵45,000.00
13.
A man bought a car for ₵5.5 million and sold it for ₵6.5 million. Find the percentage gain.
1.54%
1.82%
15.38%
18.18%
84.44%
14.
On a map, two towns P and Q are 15.5 cm apart. The scale of the map is 1 cm: 4 km. Calculate the actual distance between P and Q.
15.5 km
31 km
46 km
60 km
62 km
15.
Expand the expression 2(3a + 2b)
6a + 2b
5a + 4b
6a + 4b
10ab
12ab
16.
Mansah obtained 150 marks out of 240 marks in an English test. What was her percentage score?
33.33%
37.5%
41.67%
62.5%
79.1%
17.
The marks obtained by six boys in a test are: 14, 20, 25, 15, 28 and 16. Find the mean mark.
19.67
22.00
23.20
26.40
28.00
18.
Which of the following is equivalent to 22 × 62
2 × 34
22 × 32
22 × 34
24 × 3
24 × 32
19.
Kwaku had 300 mangoes. He sold 240 of them. What is the percentage of the mangoes left?
8%
20%
25%
26%
80%
20.
A bag contains 5 black and 6 white balls. What is the probability of picking a white ball?
21.
Solve for h in the equation 15 – 2h = 6
–10.5
–9.0
–4.5
4.5
10.5
22.
What is the image of 3 in the mapping x → 3x + 7?
10
13
16
24
34
23.
How many faces has a closed cylindrical object?
1
2
3
4
34
24.
A graph of a straight line AB is shown below.
Use it to answer the question below
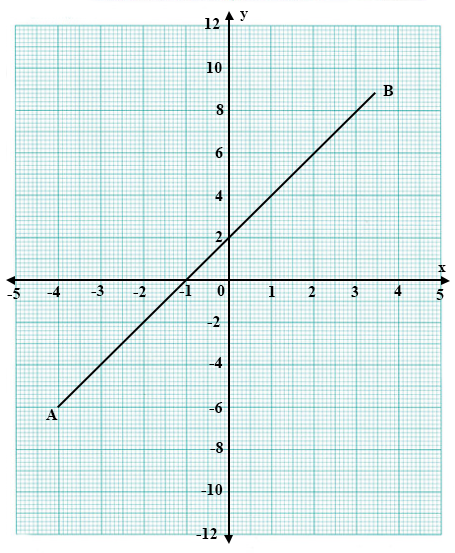
Find the gradient of the line AB
1
2
3
4
5
25.
A graph of a straight line AB is shown below.
Use it to answer the question below

Find the coordinates of the point at which the line cuts the y-axis.
(1, 0)
(0, 1)
(-1, 0)
(0, -1)
(0, 0)
26.
A man deposited an amount of ₵50,000.00 at a bank for 2 years at a rate of 20%. Find the simple interest.
₵1,000.00
₵2,000.00
₵10,000.00
₵20,000.00
₵200,000.00
27.
Kofi received ₵800.00 commission on the sales he made on a particular day. This commission is 20% of sales he made. Calculate his total sales for the day.
₵1,200.00
₵2,400.00
₵3,200.00
₵4,000.00
₵4,800.00
28.
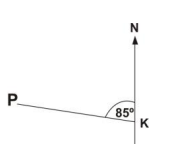
Calculate the bearing of town P from town K in the diagram below.
005°
085°
095°
265°
275°
29.
In the diagram below, PQR is an isosceles triangle. |PQ| = |PR|, ∠QPR = 40° and QRS is a straight line.
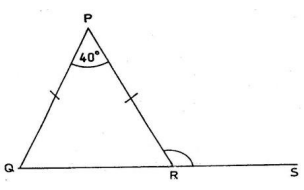
Find angle PRS.
40°
70°
100°
110°
140°
30.
Factorize completely the expression 2xy – 8x + 5y - 20.
(2x + 5)(y – 4)
(2x – 5)(y + 4)
(2x – 5)(y – 4)
(2x + 5)(y + 4)
(x + 5)(y – 4)
31.
Ama is facing east. Through how many degrees should she turn clockwise to face north?
90°
135°
180°
225°
270°
32.
In the triangle RST, ∠RST is 90°, |RS| = 4 cm and |ST| = 3 cm.
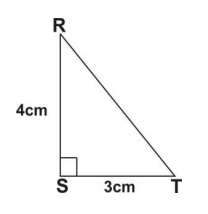
What is the length of RT?
2 cm
3 cm
4 cm
5 cm
7 cm
33.
How many lines of symmetry has a rhombus?
2
3
4
5
6
34.
Given that a = and b = .
Find b - a.
35.
If u = and v = , find 2u + v.
36.
The volume of water in a cuboid is 9 m3. The length of the cuboid is 3 m and the breadth is 2 m.
Calculate the depth of water in the cuboid.
0.15 m
0.18 m
1.5 m
1.8 m
6.0 m
37.
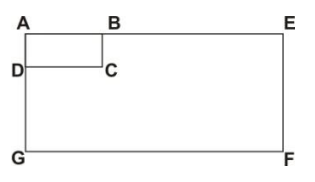
In the diagram above, rectangle AEFG is an enlargement of the rectangle ABCD. If |AB| = 5 cm and |AE| = 15 cm.
What is the scale factor of the enlargement?
2
3
10
38.
In the diagram, O is the centre of the circle and r is its radius.
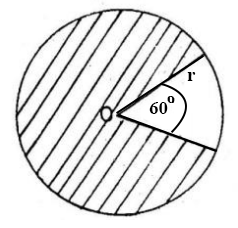
Calculate the area of the shaded region.
πr2
πr2
πr2
πr2
πr2
39.
Which of the following best describes the statement: "The locus of points 6 cm from a fixed point O?"
A parallel line 6 cm from O
A vertical line 6 cm from point O
A horizontal line 6 cm from point O
An equilateral triangle of side 6 cm
A circle with centre O and radius 6 cm
40.
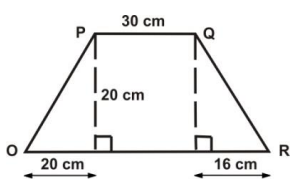
OPQR is a trapezium whose height is 20 cm. What is the area?
460 cm2
600 cm2
920 cm2
960 cm2
1000 cm2
(a)
Simplify the expression 3x2 + 6xy – 3y2 + 4x2 + 8xy + 2y2
(b)
(i)
Solve 3x – 9 ≥ 12 (x – 3)
(ii)
Illustrate your answer on the number line.
(c)
If p = 7, a = 16, b = 4 and c = 3, evaluate p2 -
(a)
Using a ruler and a pair of compasses only,
(i)
construct a triangle PQR such that |PQ| = 8 cm, angle RPQ = 90° and angle PQR = 30°. Measure |RQ|
(ii)
construct the perpendicular bisector (mediator) of RQ. Let it meet RQ at O.
(b)
With O as centre and radius OP, draw a circle. Measure |OP|.
(c)
What is the special name for the chord RQ?
(a)
A man travelled from Bakwa to Pabam. The distance between the two towns is 510 km. At Pabam he covered additional 40 km on official duties. He returned to Bakwa the next day.
(i)
Find the total distance covered by the man
(ii)
If the car used one litre of petrol to cover 20 km, find the amount of petrol used for the whole journey.
(iii)
If a litre of petrol cost ₵522.00, calculate the total cost of petrol used for the whole journey.
(b)
A woman sold an article for ₵200,000.00. She made a profit of 25%. Find the cost price of the article
(a)
The pie chart shows angles representing the number of candidates who applied for admission into four programmes at a senior secondary school. The number of pupils who applied were 1080.
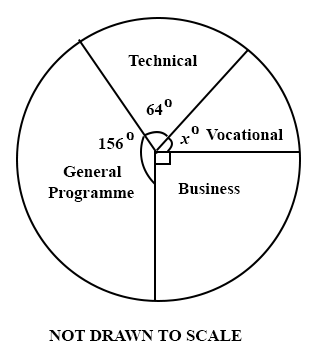
Find:
(i)
the angle x° representing the Vocational programme.
(ii)
the number of candidates who applied for Business programme.
(iii)
correct to the nearest whole number the percentage of the number of applicants who applied for General Programme.
(b)
The data below shows the distribution of the masses of pupils in a school. On a graph paper, draw a bar chart for the distribution.
| Mass (kilograms) | 19 | 20 | 21 | 22 | 23 | 24 |
| Frequency | 5 | 9 | 19 | 25 | 18 | 4 |
(a)
Using a scale of 2 cm to 2 units on both axes, draw two perpendicular axes OX and OY on a graph sheet. On the same graph sheet, mark the x-axis from –8 to 8 and the y-axis from –8 to 8
(i)
Plot P(-2, 3) and Q(6, 4). Join PQ
(ii)
Draw the image P1Q1 of PQ under an anticlockwise rotation through 90° about the origin, where P→P1 and Q→Q1. Indicate clearly all the co-ordinates.
(iii)
Draw the image P2Q2 of PQ under a clockwise rotation through 90° about the origin where P→P2 and Q→Q2. Indicate clearly all the co-ordinates
(b)
The base radius of a closed cylinder is 4 m. The height of the cylinder is 7 m. Calculate its total surface area.
[Take π = ]