1.
Set A is called ...... of set B, when all the numbers of set A are also members of set B.
the universal set
the union set
the null set
a subset
an empty set
2.
M = {multiples of 3 between 10 and 20}
N = {even numbers between 10 and 20}.
Find M ∩ N.
{12, 18}
{12, 15, 18}
{12, 14, 16, 18}
{12, 14, 15, 16, 18}
{10, 12, 14, 15, 18, 20}
3.
Express 24 as a product of prime factors.
2 × 3
22 × 3
23 × 3
22 × 32
22 × 33
4.
Write in standard form 1342.
0.1342 x 10-3
0.1342 x 10-4
13.42 x 102
1.342 x 103
1.342 x 104
5.
Change 10111two to base ten.
15
17
23
25
29
6.
If Y = 595 and Z = 7071, find the sum of Y and Z.
6466
7566
7666
12,021
13,021
7.
Simplify: - +
8.
A ribbon is 4 m long. How many pieces, each 30 cm long, can be cut from the ribbon?
7
11
12
13
14
9.
Find the integers within the interval 5 < x < 9
{5,6,7}
{5,6,7,8}
{5,6,7,8,9}
{6,7,8}
{6,7,8,9}
10.
Calculate, correct to two decimal places, 0.61 ÷ 0.8
0.07
0.08
0.76
0.83
7.62
11.
The diagram below shows a circle with centre O, S and T are points on the circle.
Use it to answer the question below
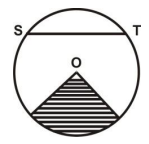
What name is given to the shaded region?
sector
segment
radii
arc
cone
12.
The diagram below shows a circle with centre O, S and T are points on the circle.
Use it to answer the question below

The line ST is called
an arc
a chord
a diameter
a radius
a segment
13.
Simplify: 2 × 32 × 34
2 × 35
2 × 36
2 × 38
2 × 96
2 × 98
14.
Which of the following fractions is the greatest? , , , ,
15.
The sum of the ages of a man and his wife is 81 years. The ratio of their ages is 5:4. Find the age of the younger person.
30 years
36 years
45 years
51 years
65 years
16.
A car is travelling at 40 km per hour. How far does it travel in 2 hours?
16 km
80 km
90 km
100 km
140 km
17.
There are 6 girls and 18 boys in a class. What percentage of the class are girls?
14.40%
25.00%
33.33%
66.67%
75.00%
18.
Find the missing numbers in the sequence 4, 8, 12, _ , _ , _ , 28
14, 16, 22
14, 18, 22
6, 18, 22
16, 20, 24
16, 22, 24
19.
A shop increased all its prices by 10%. Calculate the new price for an article which previously sold for ₵7,500.00
₵6,750.00
₵7,575.00
₵7,800.00
₵8,250.00
₵8,350.00
20.
Simplify: 7(y + 1) – 2(2y + 3)
3y – 5
3y – 2
3y + 1
3y + 4
3y + 13
21.
The table below shows the average monthly rainfall at Nankese from March, 1996 to August, 1996.
| Month | Mar | Apr | May | Jun | Jul | Aug |
| Rainfall (mm) | 99 | 145 | 227 | 450 | 267 | 142 |
Use it to answer the question below.
Which month recorded the highest amount of rainfall?
March
April
May
June
July
22.
The table below shows the average monthly rainfall at Nankese from March, 1996 to August, 1996.
| Month | Mar | Apr | May | Jun | Jul | Aug |
| Rainfall (mm) | 99 | 145 | 227 | 450 | 267 | 142 |
Use it to answer the question below.
What was the total amount of rainfall recorded in April, May and July?
422 mm
639 mm
72 mm
994 mm
1,139 mm
23.
Find the median of the following numbers: 1, -1, -5, 3 and -4
–1
–4
–5
1
3
24.
There are 15 red and 25 black balls in a bag. Find the probability of selecting a black ball from the bag.
25.
In the diagram below, K is an enlargement of J. Use it to answer the question below.
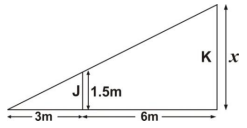
Calculate the scale factor
2
3
9
26.
In the diagram below, K is an enlargement of J. Use it to answer the question below.

Find the value of x.
3.0 m
3.5 m
4.5 m
6.0 m
9.0 m
27.
A trader received a commission of 25% on the sales he made in a month. His commission was ₵180,000.00. Find his total sales for the month.
₵135,000.00
₵150,000.00
₵240,000.00
₵540,000.00
₵720,000.00
28.
Kwame travelled from Accra to Kumasi. He travelled of the journey by lorry, of the journey by taxi and the rest by train. What fraction of the journey did he travel by train?
29.
If 4(m + 4) = 18, find the value of m.
30.
Use the mapping below to answer the question below
| x | 1 | 2 | 3 | 4 |
| ↓ | ↓ | ↓ | ↓ | ↓ |
| y | 3 | 5 | 7 | 9 |
What is the rule for the mapping?
x→ 4 - x
x→ x - 2
x→2x
x→2x + 1
x→3x
31.
Use the mapping below to answer the question below
| x | 1 | 2 | 3 | 4 |
| ↓ | ↓ | ↓ | ↓ | ↓ |
| y | 3 | 5 | 7 | 9 |
Find the value of y when x is 7.
–3
9
14
15
21
32.
A square of side 6cm has the same area as a rectangle of length 9 cm. Find the breadth of the rectangle.
3 cm
4 cm
6 cm
24 cm
36 cm
33.
Factorize 3r2s – 9rs2
rs(3r – s)
3rs(s – 3r)
3rs(r - 3s)
r2s2(3r – 9s)
3r2s2(s – 3r)
34.
The average mass of 4 boys is 45 kg. When a fifth boy joins them, the average mass changes to 40 kg. What is the mass of the fifth boy?
5 kg B
10 kg
15 kg
20 kg
25 kg
35.
E is the point (4, 2) and F the point (2, 1). Calculate the gradient of the straight line EF.
-
-2
2
0
36.
L = and K = .
Find L + K.
37.
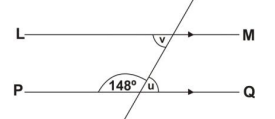
In the diagram, ML and PQ are parallel lines.
Find the value of v
32°
40°
58°
140°
180°
38.
Given the relation = + .
Which of the following expressions is equal to y?
39.
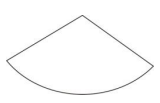
The figure above is the net of
a cylinder
a triangle
a pyramid
a cone
a sphere
40.
In the diagram below, MNO is a triangle. Angle MON = 72° and angle OMN = 68°.
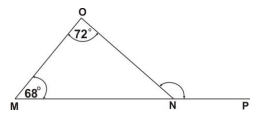
Find angle ONP.
40°
68°
72°
112°
140°
(a)
Kofi and Kojo were given ₵38,000.00 to share. Kojo had ₵7,500.00 more than Kofi. Find
(i)
Kofi's share
(ii)
Kojo's share
(b)
A trader paid ₵1500.00 for 6 drinking cups. One of the cups got broken. He sold the remaining 5, making a profit of 10%.
Calculate
(i)
the cost price of each of the six cups;
(ii)
the selling price of each of the five cups;
(iii)
the profit made on each cup sold.
(a)
Solve the inequality - > 1
(b)
Find the value of the expression 2x - 3y if x = and y = -.
(c)
25 students in a class took an examination in Mathematics and Science. 17 of them passed in Science and 8 passed in both Mathematics and Science. 3 students did not pass in any of the subjects.
Find
(i)
how many passed in Mathematics;
(ii)
the probability of meeting a student who passed in one subject only.
(a)
Using a pair of compasses and a ruler only,
(i)
construct triangle ABC such that |AB| = 10 cm, angle ABC = 30° and |BC| = 8 cm. Measure angle ACB.
(ii)
construct a perpendicular from C to meet line AB at D. Measure |CD|.
(b)
Calculate the area of triangle ABC.
(a)
(i)
Using a scale of 2cm to 2 units on both axes, draw two perpendicular axes OX and OY on a graph sheet.
(ii)
On the same graph sheet, mark the x-axis from –10 to 10 and the y-axes from –12 to 12.
(iii)
Plot the points A(0, 10), B(-6, -2), C(4, 3) and D(-3,-11).
Use a ruler to join the point A to B and also point C to D.
(b)
(i)
Draw the line x = -2 to meet AB at P and CD at Q.
(ii)
Use a protractor to measure angles BPQ and PQC.
(iii)
What is the common name given to angles BPQ and PQC?
(iv)
State the relationship between lines AB and CD.
The table below shows the marks scored out of 10 by some candidates in a test.
| Mark | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of candidates | 2 | 3 | 5 | 7 | 8 | 13 | 7 | 5 |
(a)
From the table, find
(i)
the modal mark;
(ii)
how many candidates took the test;
(iii)
the mean mark for the test.
(b)
If 20% of the candidates failed,
(i)
how many failed?
(ii)
What is the least mark a candidate should score in order to pass?