1.
M = {1, 2, 3, 8, 10} and N = {8, 1, x, 3, 2}.
If M is equal to N, what is the value of x?
1
2
3
8
10
2.
In the Venn diagram Q is the set of numbers inside the circle and R is the set of numbers inside the triangle.
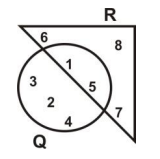
Find Q ∩ R.
{1, 5}
{2, 3, 4}
{6, 7, 8}
{1,2,3,4,5}
{1,2,3,4,5,6,7,8}
3.
Simplify: 11 – (11 – 4) + 13.
–7
–17
9
17
31
4.
What is the value of ‘4’ in the number 2,043,507?
Forty
Four hundred
Four thousand
Forty thousand
Four hundred thousand
5.
Which of the following is true?
{0, 2, 6, 9, 12} is a subset of even numbers.
{-1, 0, 2, 3, 5} is a subset of odd numbers.
{-2, -1, 1, 3, 9} is a subset of integers.
{2, 3, 5, 7, 27} is a subset of prime numbers.
{9, 18, 21, 27, 36} is a subset of multiples of 9.
6.
If (23 × 82) × 79 = 148,994, find the exact value of (2.3 × 82) × 7.9
1.48994
14.8994
148.994
1489.94
14899.4
7.
Convert 206 to a base five numeral.
411five
4011five
3321five
1311five
1131five
8.
Which of the following inequalities is represented by the number line?
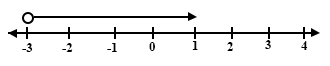
x ≤ -3
x ≥ -3
x < -3
x > -3
x = -3
9.
The product of three numbers is 1197. Two of the numbers are 3 and 21. Find the third number.
19
57
63
399
1134
10.
Simplify: - .
11.
A pencil sells at ₵180.00 and an eraser sells at ₵120.00. how much will you pay if you buy three pencils and four erasers?
₵1,020.00
₵1,080.00
₵1,200.00
₵1,280.00
₵2,100.00
12.
Simplify
0.4
0.04
0.004
0.0004
0.00004
13.
How many lines of symmetry has a square?
2
3
4
6
8
14.
In the diagram, MNO is a right angled triangle. |MO| = 13 cm and |MN| is 5 cm.
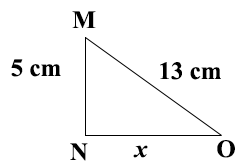
Find the value of x.
3
4
8
12
18
15.
Amina spends of her pocket money on transport and food. If she spends on transport only, what fraction does she spend on food?
16.
If x →3x – 4, what is the image of –2?
–10
–2
–1
2
10
17.
Simplify: (2ab2) (3a2b)
5a2b2
6a2b2
5a2b3
6a3b2
6a3b3
18.
It takes 15 men, 48 days to weed a plot of land. How many men can weed the same plot of land in 16 days, if they work at the same rate?
5
18
32
45
48
19.
The ratio 9 : x is equivalent to 36 : 20. What is the value of x?
4
5
6
8
10
20.
In an enlargement, PQ→P′Q′. |PQ| = 3 cm and |P′Q′| = 15 cm. Calculate the scale factor of the enlargement.
5
10
45
21.
Simplify: 7a – 3(b – a)
4a – 3b
6a – 3b
8a – 3b
10a – 3b
10a + 3b
22.
A man deposited an amount of money in his savings account for 5 years. The rate of interest was 14% per annum. If the interest was ₵35,000.00, find the amount deposited.
₵85,000.00
₵50,000.00
₵39,900.00
₵24,500.00
₵15,000.00
23.
Arrange the following fractions from the lowest to the highest: , and .
, ,
, ,
, ,
, ,
, ,
24.
The marked price of a radio set is ₵450,000. A discount of 5% of the marked price is allowed. What is the selling price of the radio set?
₵427,000
₵427,500
₵428,571
₵472,500
₵473,684
25.
If 60% of the pupils in a school is 240, find the total enrolment in the school.
144
160
360
384
400
26.
If a * b = 2a – b, evaluate 4 * 3
1
2
3
4
5
27.
The bar chart shows the mark distribution of pupils in a test. Use it to answer the question below
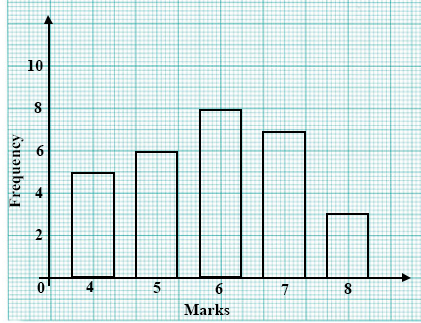
What is the modal mark?
4
5
6
7
8
28.
The bar chart shows the mark distribution of pupils in a test. Use it to answer the question below

How many pupils took the test?
5
20
25
29
30
29.
A school has a population of 600. Out of this, 120 are girls. What is the probability of meeting a pupil in the school who is a boy?
30.
If = + , find k when k1 = 1 and k2 = 2.
2
3
31.
Solve the equation 13x – 2(3x + 4) = 22.
2
4
32.
A rectangular tank is 4 m long, 3 m wide and 2.5 m high. What is the volume of the tank?
24 m3
30 m3
36 m3
48 m3
60 m3
33.
Write the rule for the mapping:
| x | 1 | 2 | 3 | 4 |
| ↓ | ↓ | ↓ | ↓ | ↓ |
| y | 1 | 3 | 5 | 7 |
x→2x + 1
x→2x - 1
x→2(x + 1)
x→2(x - 1)
x→x2- 1
34.
If r = and s = , calculate 2r - 3s.
35.
Name the geometrical figure shown in the diagram below.
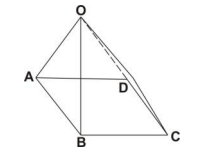
parallelogram
triangle
cone
tetrahedron
pyramid
36.
A car travels 72 kilometres in an hour. Find its speed in metres per second.
5 ms-1
20 ms-1
50 ms-1
200 ms-1
1200 ms-1
37.
The circumference of a circular track is 154 m. Find the diameter of the track.
[Take π = ]
22.0 m
24.5 m
49.0 m
242.0 m
484.0 m
38.
Find the value of the angle marked y in the diagram.
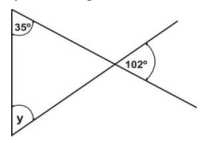
35°
43°
67°
78°
137°
39.
Which of the following best describes the construction in the diagram?
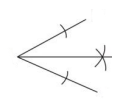
Constructing a 30° angle.
Constructing a 60° angle.
Bisecting a line segment.
Bisecting a given angle.
Drawing a perpendicular from a given point.
40.
Ama is N years old now. How old will she be in 10 years?
(N – 10) years
(N + 10) years
(10 – N) years
10 N years
years
(a)
Simplify: of 6 ÷ .
(b)
Solve the equation (x + 3) - 2(x - 5) = 4.
(c)
If 3y = 2x2 - 3x + 7, find y, when x = 5
(a)
In the diagram, PADQ and RBCS are parallel lines. │BD│ = │DC│, angle ADB = 65° and angle ABR = 50°.
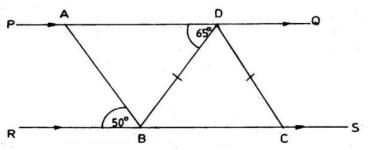
(i)
Calculate the angle BDC.
(ii)
Calculate angle ABD.
(iii)
Find angle BAD.
(iv)
What type of triangle is triangle ABD?
(b)
Using a ruler and a pair of compasses only, construct triangle XYZ, with |YZ| = 8 cm, angle XYZ = 60° and |XY|=9 cm.
Measure
(i)
angle YZX;
(ii)
|XZ|
Ama was granted a loan of ₵800,000.00 by a bank. The rate of interest was 42% per annum.
(a)
Calculate
(i)
the interest at the end of the year;
(ii)
the total amount Ama had to pay at the end of the year.
(b)
Ama was able to pay only ₵700,000.00 at the end of the year.
(i)
Find how much Ama still owed the bank.
(ii)
Express the amount Ama owed after paying the ₵700,000.00 to the bank as a percentage of the loan she took from the bank.
The following is a record of scores obtained by 30 JSS form 2 pupils in a test marked out of 5.
| 5, | 3, | 2, | 4, | 5, | 2, | 4, | 3, | 1, | 1 |
| 3, | 4, | 2, | 3, | 4, | 5, | 3, | 4, | 3, | 2 |
| 4, | 3, | 1, | 2, | 2, | 3, | 3, | 2, | 4, | 3 |
| Score (x) | Tally | Frequency (f) | fx |
(a)
Copy and complete the table.
(b)
Find the mean of the distribution.
(c)
If a pupil is selected at random from the form, what is the probability that he/she scored 4 marks?
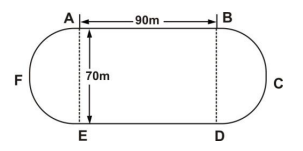
The diagram shows a running track ABCDEFA. AB and ED are the straight sides. The ends AFE and BCD are semi circular shapes.
|AB| = |ED| = 90 m and |AE| = |BD| = 70 m.
Find
(a)
the total length of the two semi circular ends, AFE and BCD;
(b)
the perimeter of the running track ABCDEFA;
(c)
the total area of the running track ABCDEF.
[Take π = ]