1.
State the property used in the operation a(b+c) = ab + ac.
Associative
Distributive
Commutative
Universal
2.
Simplify 0.1 x 0.02 x 0.003 (leaving your answer in standard form)
6x10-7
6x10-6
6x105
6x106
3.
Express as a decimal fraction.
0.4
0.04
0.004
0.0004
4.
In an examination, 25% of the candidates failed to obtain the pass mark. The number of candidates who passed was 150. How many candidates failed?
113
100
50
38
5.
How many faces has a cube?
8
6
5
4
6.
Simplify 28 ÷ 23
224
210
25
23
7.
The Venn diagram below shows the number of pupils in a class of 40, who speak Twi or Ga or neither.
Use it to answer the question below.
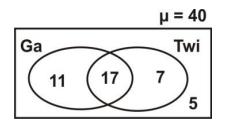
How many pupils speak Twi and Ga?
17
11
7
5
8.
Use it to answer the question below.

How many pupils speak neither Twi nor Ga?
17
11
7
5
9.
Find the least common multiple (LCM) of the numbers 10, 15 and 25.
30
60
120
150
10.
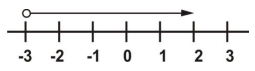
Which of the following expression is illustrated on the number line above?
x < -3
x ≤ -3
x > -3
x ≥ -3
11.
Simplify -
12.
Correct 0.00025 to one significant figure.
0.2
0.003
0.0002
0.0003
13.
If y : 28 = 5 : 7, find y.
5
20
31.2
37.5
14.
Convert 121five to a base ten numeral.
21
35
36
40
15.
Find the image of 4 under the following mapping.
| x | 1 | 2 | 3 | 4 | 5 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| y | 4 | 7 | 10 | k | 16 |
11
12
13
14
16.
The point K(3, 4) is rotated through 180° about the origin. Find its image.
(-3, 4)
(-4, 3)
(-3, -4)
(3, -4)
17.
Arrange the following fractions in descending order of magnitude: , ,
, ,
, ,
, ,
, ,
18.
Which of the following best describes the construction below?
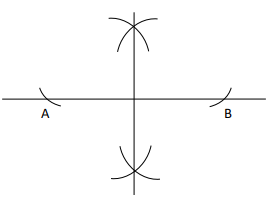
Constructing an angle of 60°
Constructing the perpendicular bisector of AB
Constructing a circle about the midpoint of AB
Constructing an angle of 180°
19.
Find the image of the point K (3, 5) when it is reflected in the x-axis.
(3, 5)
(5, 3)
(3, -5)
(-3, -5)
20.
A set of furniture was sold for ₵300,000.00 at a profit of 20%. Find the cost price.
₵250,000
₵240,000
₵200,000
₵180,000
21.
Make x the subject of the relation, v2 = u2 + 2ax.
x = u2 + 2av2
x =
x =
x =
22.
Three baskets contain 95 oranges, x oranges and 2x oranges. How many oranges are in the three baskets?
96x
95 + 3x
95 + 2x2
98x
23.
The pie chart shows the distribution of programmes offered by 720 students at Kofikrom.
Use this information to answer the question below.
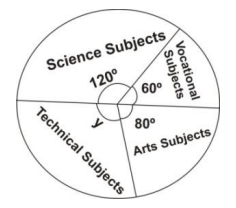
Find the value of the angle marked y.
90°
100°
110°
120°
24.
The pie chart shows the distribution of programmes offered by 720 students at Kofikrom.
Use this information to answer the question below.

How many more students offered science subjects than Arts subjects.
40
80
160
240
25.
Kofi is two years older than Ama. If the sum of their ages is 16, find Ama's age.
7 years
9 years
14 years
18 years
26.
J = mv2, If v = 4 and J = 12, find m
1.5
3.0
3.6
6.3
27.
PQR is a right-angled triangle. The area of the triangle is 6 cm2 and |QR| = 3 cm.
Find |PR|.
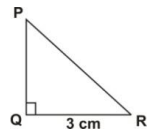
2 cm
3 cm
5 cm
6 cm
28.
A rectangle has a length of 8 cm and a breadth of 6 cm. How long is its diagonal?
10
14
28
50
29.
Simplify (2 + )
30.
A man divided his 360 cattle among his three sons in the ratio 7 : 6 : 5. How many cattle did the one who had the smallest share receive?
100
120
140
160
31.
The marks obtained by 9 students in a test are 3, 3, 4, 5, 6, 7, 7, 7, 8.
Use this information to answer the question below.
Find the median
4
5
6
7
32.
The marks obtained by 9 students in a test are 3, 3, 4, 5, 6, 7, 7, 7, 8.
Use this information to answer the question below.
What is the mode?
3
4
6
7
33.
What is the fifth term of the sequence , , ...?
34.
30 men dig a pit in 21 days. How many days will 14 men take to dig the pit, working at the same rate?
20
25
30
45
35.
A bag contains 6 white and 8 red balls. What is the probability that a ball picked at random will be a white ball?
36.
The figure below is a cuboid wih dimensions x cm by y cm by z cm. Find the area of the face PQRV.
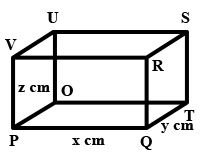
xy cm2
yz cm2
x2 cm2
xz cm2
37.
A rod 200 cm long is broken into two parts. The shorter part is one-quarter of the length of the rod. Express the shorter part as a percentage of the longer part.
25%
30%
33.33%
66.67%
38.
In the figure below, MN and PQ are straight lines. Find the value of the angle marked x in the figure.
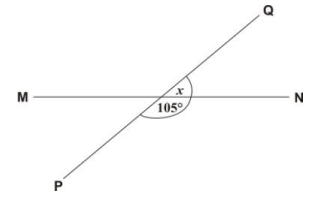
65°
75°
85°
155°
39.
Find the value of x in the equation = 2
2
4
6
8
40.
The circumference of a circular track is 15.4 m. Find the diameter of the track.
[Take π = ]
4.9 m
22 m
24 m
24.5 m
(a)
Simplify 2 ÷
(b)
There are 50 pupils in a class. Out of this number, speak French only and of the remainder speak both French and English. If the rest speak English only,
(i)
find the number of students who speak
(α)
both French and English;
(β)
only English.
(ii)
Draw a Venn diagram to illustrate the above information.
A shop sells a pencil at ₵500.00 and a pen at ₵2,000.00
(a)
If Afua bought 8 pencils and 5 pens, how much did she pay together for them?
(b)
The price of a pencil is increased by 20% and a pen by 10%. Find how much she will pay for 10 pencils and 8 pens.
(a)
Using a ruler and a pair of compasses only, construct
(i)
triangle ABC such that AB = 12cm, AC = 8cm and BAC = 30°;
(ii)
a perpendicular from C to meet AB at M.
(b)
Measure
(i)
angle ABC;
(ii)
|CM|.
(c)
Calculate the area of triangle ABC.
(a)
Solve the inequality - < 2
(b)
(i)
Copy and complete the table of values for he relation, y = 2x + 1
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -5 | -3 | 1 | 7 |
(ii)
Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 units on the y-axis, plot the ordered pairs (x, y) on a graph sheet.
(iii)
Use a ruler to join the joints plotted.
(iv)
Use your graph to find
(α)
x when y = 4
(β)
y when x = -2.5
The table shows the number of students in a JSS class who prepared various dishes for their practical.
| Dishes | No. of students |
| Fufu and light soup | 5 |
| Banku and Okro stew | 20 |
| Fried rice | 30 |
| Fried plantain and beans | 25 |
| Boiled yam and palaver sauce | 10 |
(a)
(i)
Draw a pie chart for the distribution above.
(ii)
What dish was prepared most?
(iii)
What percentage of students prepared fried rice
(b)
What is the probability that a student chosen at random cooked fried plantain and beans?