1.
If the set A = {1, 2, 3, 4, 5} and the set B = {2, 4, 6}, find the number of members in the set A U B.
8
6
5
2
2.
How many faces has a cuboid?
3
4
5
6
3.
Evaluate
0.018
0.18
1.8
18.0
4.
The angle formed by one complete revolution is equivalent to
one right angle
two right angles
three right angles
four right angles
5.
If the set P = {1, 2, 3, 4, 5} which of the following statements best describes P?
Set of whole numbers up to 6
Set of counting numbers less than 6
Set of counting numbers greater than 6
Set of integers less than 6
6.
Which of the following numbers is the next prime number greater than 23 ?
17
24
25
29
7.
Simplify -35 – (-15) + (-30)
17
–50
50
30
8.
Write 78910 correct to the nearest thousand.
70,000
78,000
79,000
80,000
9.
Simplify
33 x 24
10.
Which of the following inequalities is represented on the number line below?
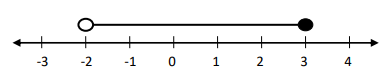
-2 < x < 3
-2 ≤ x < 3
-2 ≤ x ≤ 3
-2 < x ≤ 3
11.
Factorize completely the expression 4xy - 16x + 10y – 40.
(y + 4) (4x – 10)
(y – 4) (4x + 10)
(4 – y) (10 – 4x)
(y + 4) (4x + 10)
12.
What is the image of 2 in the mapping x → 2x + 5?
7
9
12
20
13.
Simplify 3a2b3 × 4a3b.
12a5b4
12a4b5
7a5b4
7a4b5
14.
Find the solution set of 2x + 1 < 5 in the domain {-1, 0, 1, 2, 3}.
{-1, 1, 3}
{-1, 0, 1}
{-1, 1, 2}
{0, 1, 2}
15.
Find the highest common factor (HCF) of 48, 60 and 96.
12
24
36
48
16.
P = {odd numbers between 20 and 30} and Q = {23, 29}. Which of the following is true?
P ⊂ Q
Q ⊂ P
P = Q
P ∩ Q = Φ
17.
Find the rule for the following mapping:
| x | 0 | 1 | 2 | 3 | 4 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| y | -1 | 1 | 3 | 5 | 7 |
y = 2x + 1
y = 2x – 1
y = x2-1
y=x2+1
18.
If a = and b = , find 2a - b.
19.
Find the value of x in the polygon below
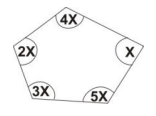
12°
36°
60°
72°
20.
An article costs ₵60,000.00. The price was increased by 10%. Find the new price.
₵54,000.00
₵61,000.00
₵66,000.00
₵70,000.00
21.
Solve for x in the equation 15 – 2x = 6
–10.5
–4.5
4.5
10.5
22.
The population of Ghana was 5,000,000 in 1957. The population in 1998 was estimated to be 17,000,000. Find the percentage increase in population from 1957 to 1998.
2.4%
24%
240%
2400%
23.
The angles of a triangle are in the ratio 3 : 2 : 1. Find the value of the smallest angle.
30°
45°
60°
90°
24.
Find the least common multiple (LCM) of 4, 6 and 10
10
24
30
60
25.
Convert 134five to a base ten numeral
16
40
44
220
26.
A circle has radius 7cm; find its area.
[Take π = ]
22 cm2
44 cm2
145 cm2
154 cm2
27.
Simplify - +
28.
Solve for x, if x - 4x > 20
x < -13
x< -5
x > 5
x > 13
29.
Which of the following is equivalent to 22 × 63?
26 × 33
25 × 33
24 × 3
23 × 33
30.
The volume of water in a rectangular tank is 30 cm3 .The length of the tank is 5 cm and its breadth is 2 cm. Calculate the depth of water in the tank.
4.0 cm
3.0 cm
5.0 cm
6.0 cm
31.
The following temperatures in oC were recorded in 10 cities in Europe; -4, 5, 2, 0, -6, -4, 3, -6, -4, 7.
Find the modal temperature.
–2°
–4°C
0°C
–6°C
32.
The ratio of the ages of two sisters is 4 : 3. The elder sister is 3 years older than the younger one. How old is the younger sister?
9 years
12 years
15 years
18 years
33.
If n2 + 4 = 40, find n.
6
18
22
44
34.
An angle which is more than 90° but less than 180° is
an acute angle
a right angle
an obtuse angle
a reflex angle
35.
Arrange the following fractions in ascending order: 4, 4, 4
4, 4, 4
4, 4, 4
4, 4, 4
4, 4, 4
36.
Prices of items in a shop were reduced by 10% during a reduction sale. If a customer bought an electric fan for ₵81,000.00, what was its original price?
₵72,900.00
₵73,900.00
₵89,100.00
₵90,000.00
37.
The marks scored by 8 pupils in a science test are: 3, 7, 8, 8, 5, 4, 8, 4.
Use it to answer the question below.
What is the median mark?
5
6
7
8
38.
The marks scored by 8 pupils in a science test are: 3, 7, 8, 8, 5, 4, 8, 4.
Use it to answer the question below.
What is the probability that a pupil chosen at random scored 4 marks?
39.
If y = k + ax2, find y when k = , a = and x = 2.
30
7
6
4
40.
Which of the following dimensions of a triangle form the sides of a right angled triangle?
3cm, 4cm, 6cm
3cm, 5cm, 7cm
5cm, 12cm, 13cm
5cm, 13cm, 17cm
(a)
(i)
Factorize completely the expression 2xy – 8x + 3y – 12
(ii)
Evaluate the expression in (i) if x = 5 and y = 7
(b)
Make q the subject of the equation t = +
(c)
Given that U = and V = , find 3(U + V).
(a)
Ama and Kofi shared the profit earned from their business in the ratio 3 : 4. The profit was ₵1,743,000.00
(i)
Find how much of the profit each person received.
(ii)
Kofi lent out his share of the profit at a rate of 20% per annum for 2 years. Find the interest on his share.
(iii)
What will be Kofi's total amount at the end of the 2 years?
(b)
Change 243five to a base ten numeral.
(a)
Using a ruler and a pair of compasses only, construct,
(i)
triangle PQR such that |PQ| = 8cm, angle QPR = 60° and angle PQR = 45°.
(ii)
Measure |QR|.
(b)
A rectangular water tank has length 60cm, width 45cm and height 50cm.
Find
(i)
the total surface area of the tank when closed
(ii)
the volume of the tank
(iii)
the height of the water in the tank, if the tank contains 81,000 cm3 of water.
(a)
A car runs on the average at 45 km to 5 litres of fuel. Calculate how many litres of fuel are required for a journey of 117 km.
(b)
(i)
Solve for x in the inequality (2x + 5) ≤ 8
(ii)
Illustrate the solution on the number line.
(c)
A factory increased its production by 22% and produced 49,000 tonnes. How many tonnes was it producing before?
(a)
(i)
Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes OX and OY on a graph sheet.
(ii)
On the same graph sheet, mark the x-axis from –5 to 5 and the y-axis from –6 to 6.
(b)
Plot the points,
(i)
P(1, -2) and Q(4, 5)
(ii)
P′ the image of P under a translation by the vector and Q′, the image of Q by the same vector.
(c)
(i)
Join PQQ′P′.
(ii)
Measure angles PQQ′ and PP′Q′.
(d)
(i)
Find the vectors PQ→ and P′Q'→
(ii)
What is the shape of PQQ′P′?
(a)
The following are the ages in years of members of a group: 8, 11, 8, 10, 6, 7, 3x, 11, 11.
If the mean age is 9 years, find
(i)
x
(ii)
the modal age
(iii)
the median age.
(b)
Draw a bar chart for the distribution