1.
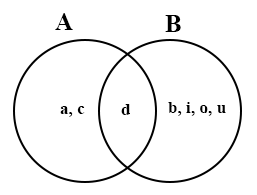
In the diagram above, A and B are two intersecting sets. How many members are in the set B?
2
3
5
7
2.
Which of the following is not a factor of 18?
3
4
6
9
3.
Multiply 0.014 by 0.2
0.00028
0.0028
0.028
0.28
4.
Given that A = {b, c, i} and B = {a, e, f, i}, find A ∩ B.
{a, b, c, e, f, i}
{f, i}
{a}
{i}
5.
If a = 64 and b = 22, find .
32
16
6.
Arrange the following numbers from the highest to the lowest: , -7, 0.
-7, 0,
-7, , 0
0, , -7
, 0, -7
7.
Simplify 22 × 32 × 23 × 34.
22 × 36
24 × 37
25 × 36
26 × 38
8.
In an examination 40% of the students failed. The number of students that passed was 180. How many students failed?
120
270
300
450
9.
Evaluate [(5 – 1) – (2 – 7)]
-3
-1
1
3
10.
If 6n + 4 = 16, find the value of n.
2
3
5
6
11.
What is the next term in the following set of numbers: {1, 3, 7, 15, 31, ...} ?
35
39
47
63
12.
Find the mean of the following set of numbers 10, 12, 14 and 16.
12
13
14
15
13.
Simplify 3a2 × 2ab × 4bc
9a3b2c
12a2b2c
24a2b2c
24a3b2c
14.
Expand 3 (2a + 3b)
2a +9b
5a + 6b
6a + 3b
6a + 9b
15.
Find the area of a circle whose diameter is 28 cm.
[Take π = ]
44 cm2
88 cm2
352 cm2
616 cm2
16.
In sharing 95 oranges with Dede, Fofo kept 45 of them and shared the rest equally with Dede. How many oranges did Dede get?
20
25
40
55
17.
If c = , find c when b = 3, r = 4 and a = 5
18.
A woman bought a sewing machine for ₵800,000.00 and sold it for ₵920,000.00. Find the percentage profit
12%
13%
15%
16.4%
19.
What is the rule for the following mapping?
| x | 0 | 1 | 2 | 3 | 4 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| y | 5 | 9 | 13 | 17 | 21 |
y = x + 5
y = 4x + 5
y = 5x + 4
y = 6x + 1
20.
Find the volume of a cuboid of sides 15 m by 12 m by 3 m.
36 m3
45 m3
180 m3
540 m3
21.
A bag contains 4 blue and 8 red balls. What is the probability of picking a blue ball at random from the bag?
22.
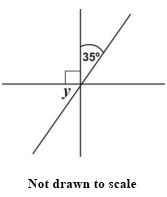
Find the size of the angle marked y in the diagram.
35°
45°
55°
90°
23.
An equilateral triangle has side 16cm. A square has the same perimeter as the equilateral triangle. What is the area of the square?
48 cm2
96 cm2
144 cm2
256 cm2
24.
Kofi deposited ₵500,000.00 with a bank for 2 years at a rate of 10% per annum. Find the simple interest
₵10,000.00
₵20,000.00
₵50,000.00
₵100,000.00
25.
Make T the subject of the relation l2 =
T =
T =
T =
T =
26.
Evaluate
0.0042
0.042
0.42
4.2
27.
Eric and Ebo are to share an amount of ₵800,000.00 in the ratio 5:3 respectively. What will be Ebo's share?
₵30,000.00
₵50,000.00
₵300,000.00
₵500,000.00
28.
How many faces has a rectangular pyramid?
4
5
6
7
29.
The perimeter of a rectangle is 24 cm. If the breadth of the rectangle is 4 cm, find the area of the rectangle.
32 cm2
48 cm2
64 cm2
144 cm2
30.
Factorize 4ab2 – 20ba2
4a(b2 – 5b)
4b(b – 5a)
4ab(b - 5a)
4ab(a - 5b)
31.
Solve the equation (x - 3) = (x + 6).
-42
-12
18
42
32.
Kofi had 100 mangoes and sold 80 of them. What is the percentage of mangoes left?
12.5%
18%
20%
25%
33.
Find the median of the following marks: 2, 4, 10, 3, 6, 12.
4
5
6
10
34.
In a class of 20 pupils, 8 pupils read Mathematics, 13 read English and 3 read both Mathematics and English.
Use this information to answer the question below.
How many pupils read English only?
2
3
5
10
35.
In a class of 20 pupils, 8 pupils read Mathematics, 13 read English and 3 read both Mathematics and English.
Use this information to answer the question below.
How many pupils do not read either Mathematics or English?
2
3
5
7
36.
Calculate 82.5 ÷ 0.25, expressing the answer in the standard form
3.3 x 10-3
3.3 x 10
3.3 x 102
3.3 x 103
37.
The price of a gas cooker costing ₵450,000.00 was increased by 10%. Find its new price.
₵45,000.00
₵49,000.00
₵405,000.00
₵495,000.00
38.
What is the number of all possible outcomes of tossing a die?
2
3
4
6
39.
In the diagram, QRS is a triangle. Angle QRS = 50° and angle RST = 120°. Find angle RQS.
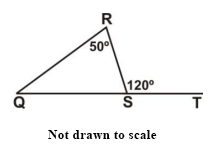
60°
65°
70°
80°
40.
If r = and s = , find r + 2s.
(a)
A boy has enough money to buy 14 pencils at ₵450.00 each. How many erasers costing ₵300.00 each can he buy with the same amount of money?
(b)
A circle has a circumference of 44cm. Calculate its radius if π =
(c)
Simplify (2 - 1) ÷ 3 .
(d)
If = 1, find n.
(a)
Copy and complete the table below for the relation: x + y = 180
| x | 0 | 30 | 60 | 90 | 120 | 150 | 180 |
| y | 180 | 90 | 0 |
(b)
(i)
Using a scale of 2 cm to 20 units on both axes, draw two perpendicular axes OX and OY.
(ii)
Mark both axes from 0 to 180.
(iii)
Plot all the seven points. Use a ruler to join all the points.
(c)
Using your graph, find
(i)
y when x = 100;
(ii)
x when y = 70.
(a)
There are 30 boys in a sporting club. 20 of them play hockey and 15 play volley-ball. Each boy plays at least one of the two games.
(i)
Illustrate the information on a Venn diagram
(ii)
How many boys play volleyball only?
(b)
Factorize xy + 3x + 6y + 18
(c)
Multiply (3 + x) by (5 – 2x)
A woman borrowed ₵2,000,000.00 from a bank at a rate of 15% per annum simple interest for 2 years.
(a)
Find
(i)
the interest for the 2 years;
(ii)
how much she paid in all to the bank after the 2 years.
(b)
She used the ₵2,000,000.00 to purchase a fridge and sold it at a profit of 45%. Find the selling price of the fridge.
(c)
If she used the amount raised from the sale of the fridge to pay for the bank loan and interest, find how much money is left.
(a)
Using a pair of compasses and ruler only, construct
(i)
triangle ABC with │AB│ = 10cm, angle ABC = 30° and angle CAB = 60° ;
(ii)
a perpendicular from the point C to meet the line AB at P.
(b)
(i)
Extend line CP to the point D such that │BC│ = │BD│.
(ii)
Join A to D and B to D.
(iii)
Measure │AC│ and │AD│.
(c)
What type of quadrilateral is ADBC?
The following marks were obtained by pupils in a test.
| 6 | 4 | 8 | 2 | 8 |
| 6 | 8 | 8 | 8 | 10 |
| 8 | 9 | 8 | 6 | 10 |
| 2 | 2 | 6 | 6 | 6 |
(a)
Construct a frequency distribution table for the data.
(b)
What is the modal mark?
(c)
Calculate the mean mark.
(d)
How many pupils scored more than 6 marks?
(e)
What is the probability that a student chosen at random obtained 2 marks?