1.
Given that A = {1, 2, 3, 4, 5, 6} and B = {3, 6, 9, 12}, find A ∪ B.
{3, 6}
{6, 12}
{2, 3, 4, 5, 9, 12}
{1, 2, 3, 4, 5, 6, 9, 12}
2.
Write 2340000 in standard form.
2.34 x 10-6
2.34 x 10-5
2.34 x 106
2.34 x 107
3.
How many faces has a cuboid?
12
8
6
4
4.
Subtract 125.47 from 203.90
78.57
78.43
-121.57
-122.38
5.
Simplify (5m + 3n)-(2m-n).
5m - 4n
3m + 4n
3m - 2n
7m + 4n
6.
Which of the following sets is equal to {1, 2, 3, 4}?
{2, 4, 1, 5}
{2, 1, 4, 3}
{1, 2, 3, 4, ...}
{2, 3, 4, 5, ...}
7.
In a town of 42,800 inhabitants, 48% are male. The rest are female. How many more females are there than males?
22,256
20,544
1,712
1,612
8.
What set does the following graph represent?
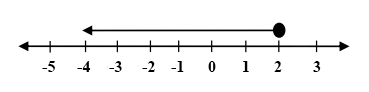
{x:x < 2}
{x:x ≤ 2}
{x:x > 2}
{x:x ≥ 2}
9.
The pie chart below shows the performance of Kate in her final examination.
Use the diagram to answer the question below.
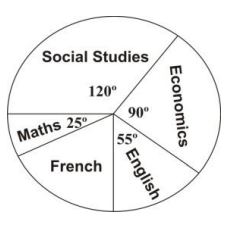
What is the angle for French?
120o
100o
70o
35o
10.
The pie chart below shows the performance of Kate in her final examination.
Use the diagram to answer the question below.

If Kate scored 60% in Social Studies, what was her score in Economics?
45%
54%
72%
90%
11.
A teacher is to be chosen at random from a group of 6 male and 2 female teachers for a patron of a Mathematics Club. What is the probability that a female teacher is chosen?
12.
Solve the equation: 2x -3(x - 1) = 6
3
-3
-7
-9
13.
If m = 3 and n = -3, evaluate (3m - n)
6
3
0
-6
14.
Which of the following sets of angles form the interior angles of a right angled triangle?
{20°, 50°, 90°}
{80°, 60°, 90°}
{45°, 45°, 90°}
{65°, 90°, 35°}
15.
State the rule for the mapping
| x | 0 | 1 | 2 | 3 | 4 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| y | 0 | 1 |
x →
x →
x →
x →
16.
A rectangle has an area of 36 cm2 and a width of 3 cm. Find its perimeter.
12 cm
18 cm
24 cm
30 cm
17.
Find the value of 4 + x0.
3
4
5
6
18.
A van travels 154 km in 1 hours. Find its speed in km/h.
77 km/h
88 km/h
100 km/h
269.5 km/h
19.
In the figure below, PQ and RS are straight lines. Find the value of the angle marked w°.
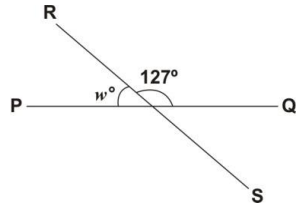
27°
53°
63°
127°
20.
If x + 5 = -7, find the value of .
-5
-2
-
2
21.
In the following diagram, rectangle OABC is enlarged into rectangle OA1B1C1 from center O. OC = 5 cm, OA = 2 cm and AA1 = 1 cm.
Use the diagram to answer the question below.
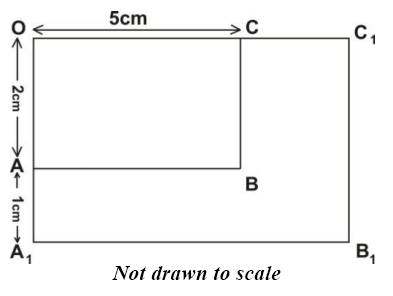
Find the scale factor of the enlargement.
1
1.5
2
2.5
22.
In the following diagram, rectangle OABC is enlarged into rectangle OA1B1C1 from center O. OC = 5 cm, OA = 2 cm and AA1 = 1 cm.
Use the diagram to answer the question below.

Calculate OC1.
7.5 cm
8 cm
9 cm
12 cm
23.
The height of a flag pole in a scale drawing is 5 cm. If the scale is 1 cm to 3 m, what is the actual height of the pole?
10 m
15 m
8 m
5 m
24.
Factorize ax + 3x + a + 3
x(a + x)
(x - a)(x + 3)
x(a - x)
(a + 3)(x + 1)
25.
If y = , find the value of y when x = 2.
5
-5
4
-4
26.
Find the Greatest Common Factor (GCF) of 90, 126 and 72.
6
9
18
24
27.
Given that 1 : 3 = x : 21, find the value of x.
4
5
7
63
28.
Find the difference between 432five and 143five
234five
334five
1130five
1310five
29.
Simplify: 14 - 2 + 5
6
7
17
17
30.
Nine bottles of equal capacity hold 4 litres of water. How much do x bottles hold?
x litres
2x litres
20x litres
40x litres
31.
A sales girl receives a 5 % commission on all she sells. Find how much she has to sell to receive GH₵ 15.00.
GH₵ 750.00
GH₵ 300.00
GH₵ 75.00
GH₵ 30.00
32.
Arrangle the following fractions in ascending order: , , ,
, , ,
, , ,
, , ,
, , ,
33.
Add 2.5 to the product of 4.2 and 0.2
13.4
10.9
3.34
1.34
34.
What is the value of four in the number 7073.48?
four tenth
four
forty
four hundred
35.
The table below shows the ages of children at a birthday party.
| Ages(years) | No. of Children |
| 1 | 3 |
| 2 | 4 |
| 3 | 2 |
| 4 | 5 |
| 5 | 4 |
| 6 | 4 |
| 7 | 6 |
| 8 | 4 |
| 9 | 2 |
| 10 | 1 |
Use this table to answer the question below.
What is the modal age?
10
7
5
4
36.
The table below shows the ages of children at a birthday party.
| Ages(years) | No. of Children |
| 1 | 3 |
| 2 | 4 |
| 3 | 2 |
| 4 | 5 |
| 5 | 4 |
| 6 | 4 |
| 7 | 6 |
| 8 | 4 |
| 9 | 2 |
| 10 | 1 |
Use this table to answer the question below.
A child is selected at random, what is the probability that he or she is 4 years old?
37.
The table below shows the ages of children at a birthday party.
| Ages(years) | No. of Children |
| 1 | 3 |
| 2 | 4 |
| 3 | 2 |
| 4 | 5 |
| 5 | 4 |
| 6 | 4 |
| 7 | 6 |
| 8 | 4 |
| 9 | 2 |
| 10 | 1 |
Use this table to answer the question below.
How many children are 7 or more years old?
28
22
13
6
38.
Write the vector using cartesian components.
39.
Simplify: 5 - 7 + 2(3 - 8)
-12
-8
-5
-4
40.
If r = and n = , find n + r.
(a)
Simplify: and write your answer in standard form.
(b)
A plot of land measures 25 m by 12 m. A portion of this plot measuring 8 m by 8 m is used for the cultivation of vegetables.
Find the area of the plot not cultivated.
(c)
The table below shows the performance of Aisha in her final examination.
| Subject | Score |
| English Language | 54% |
| Mathematics | 36% |
| Ga | 68% |
| Science | 50% |
| Social Studies | 32% |
Draw a pie chart to represent this information.
The table below shows the scores of some students in an examination.
| Scores | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Frequency | 3 | 5 | 3 | 2 | 7 | 6 | 5 | 4 | 2 | 2 | 1 |
From the table, find
(a)
how many students wrote the examination;
(b)
the modal score;
(c)
the number of students that scored 7 or more;
(d)
the mean score correct to one decimal place.
(a)
(i)
Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes OX and OY on a graph sheet.
(ii)
Mark on the same graph sheet, the x-axis from -5 to 5 and y-axis from -6 to 6.
(iii)
Plot the points A(2, 5), B(2, 2) and C(4, 2). Join the points A, B and C to form triangle ABC.
(iv)
Using the y as mirror line, draw the image triangle A1B1C1 of the triangle ABC such that A → A1, B → B1 and C → C1. Write down the coordinates of A1, B1 and C1.
(v)
Draw the image triangle A2B2C2 of triangle ABC under anticlockwise rotation of 180° about the origin where A → A2, B → B2 and C → C2. Write down the coordinates of A2, B2 and C2.
(b)
Given that a = , b = and c = , evaluate 2a - 3c + b.
(a)
The ratio of the sheep to goats on a farm is 4 : 7. If there are 1,428 sheep, find how many goats are on the farm.
(b)
Using a ruler and a pair of compasses only, construct a triangle ABC with |AB| = 6cm, |AC| = 8 cm and angle BAC = 30°. Construct the bisector of angle ACB to meet line AB at D.
(i)
Measure |AD| and |BD|.
(ii)
Write down the ratio |AD|:|BD|
(a)
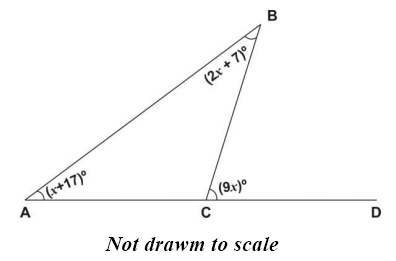
The diagram is a triangle ABC with the side AC produced to D. Find
(i)
the value of x;
(ii)
angle ACB.
(b)
The simple interest formula, I = , gives the interest, I on a principal, P invested at a rate, R per annum for time, T years.
(i)
Find the simple interest on GH₵ 3,600.00 at 15% per annum for 2 years.
(ii)
Make R the subject of the simple interest formula.
(iii)
At what rate per annum will GH₵ 6,000.00 earn GH₵ 2,400.00 simple interest in 2 years?
(a)
Given that ₵10,000 = GH₵ 1.00.
Complete the following table relating cedis (x) to Ghana cedis (y).
| ₵(x) | GH₵(y) |
| 10,000 | 1 |
| 50,000 | |
| 150,000 | |
| 250,000 | |
| 350,000 | |
| 450,000 | 45 |
(b)
(i)
On a graph sheet, draw two perpendicular axes 0x and 0y.
(ii)
Using a scale of 2 cm to ₵50,000.00 on the 0x axis and 2 cm to GH₵ 5.00 on the 0y axis, mark 0x axis from 0 to ₵500,000.00 and 0y axis from 0 to GH₵ 50.00.
(c)
Plot the points and join them with a straight line.
(d)
From your graph, find the value of
(i)
GH₵ 8.00 in cedis (₵);
(ii)
GH₵ 35.00 in cedis(₵);
(iii)
₵260,000.00 in Ghana cedis (GH₵).