1.
Which of the following sets is well defined?
{Man, Kofi, Red, 14}
{Ink, Mango, Green, Nail}
{Car, Road, Glass, Book}
{Seth, Mary, Jacob, Evelyn}
2.
If set B is a subset of set A, then
sets A and B have the same number of elements.
some members of set B can be found in set A.
no member of set B is in set A.
all the members of set B are in set A.
3.
The least common multiple (L.C.M) of 16, 30 and 36 is
3
6
240
720
4.
The sum of 5 and x divided by 4 is equal to 3.25. Find the value of x.
8
7
2
-3
5.
The numbers 32, 33, 34, ..., ..., 42 form a sequence in base 5. Find the missing numbers.
35, 36
30,31
40, 41
31, 41
6.
Write down all the integers in the set A = {-10, -4, 0, , 2, 45, 100}
{-10, -4, 0, 45, 100}
{-10, -4}
{0, 45, 100}
{, 2}
7.
Find the total cost of 25 pens and 75 books if each pen costs GH₵ 0.20 and each book costs GH₵ 0.30.
GH₵ 22.50
GH₵ 23.50
GH₵ 27.50
GH₵ 50.00
8.
Simplify: -27 + 18 - (10 - 14) - (-2)
-3
-7
-11
-35
9.
Arrange the following numbers from the lowest to the highest: 0.5, 3, -5, 0.
0, 0.5, -5, 3
0, -5, 0.5, 3
-5, 0, 0.5, 3
-5, 0.5, 0, 3
10.
Find how many pieces of cloth 5 m long that can be cut from a roll of cloth 121 m long.
665
115
66
22
11.
Find the value of 124.3 + 0.275 + 74.06, correcting your answer to one decimal place.
198.6
198.7
892.0
892.4
12.
Esi and Kwasi are 12 and 8 years old respectively. They share 60 mangoes in the ratio of their ages. How many mangoes does Esi get?
42
40
36
18
13.
It takes 6 students 1 hour to sweep their school compound. How long will it take 15 students to sweep the same compound?
24 minutes
12 minutes
3 hours
2 hours
14.
A housing agent makes a commission of GH₵ 103,500 when he sells a house for GH₵ 690,000. Calculate the percentage of his commission.
15.0 %
10.0 %
7.5 %
5.0 %
15.
A simple interest of GH₵ 37,500.00 is earned on an amount of GH₵ 500,000.00 for 3 years. Calculate the percentage rate.
20.0 %
10.0 %
5.0 %
2.5 %
16.
Simplify: (8x2y3)(xy4)
3x3y7
3x2y7
3x3y4
3xy
17.
The scores of 10 students in an examination are given as follows: 45, 12, 75, 81, 54, 51, 24, 67, 19 and 39. What is the median of the scores?
39
48
51
54
18.
The pie chart is to be drawn from the data in the following table:
| Cassava | 20% |
| Yam | 17% |
| Plantain | 28% |
| Maize | 35% |
What will be the value of the angle of the sector for maize?
126.0 o
100.8 o
72.0 o
61.2 o
19.
Eighteen cards are numbered from 11 to 29. If one card is chosen at random, what is the probability that it contains the digit 2?
20.
Find the value of x, if + 1 = 5.
24
20
19
16
21.
Factorize: xy + 5x + 2y + 10.
(x + 5)(2y + 10)
(x + 2)(y + 10)
(x + 5)(y + 2)
(x + 2)(y + 5)
22.
If x ∈ {2, 3, 4, 5}, find the truth set of 2x + 1 < 8
{2, 3, 4}
{2, 3}
{3, 4}
{4, 5}
23.
Solve the inequality: 7x - (10x + 3) ≥ -9
x ≥ 2
x ≤ 4
x ≥ 4
x ≤ 2
24.
Find the rule of the mapping:
| 1 | 2 | 3 | 4 | 5 | .... | x |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | |
| 7 | 11 | 15 | 19 | 23 | .... | y |
x → 4x - 3
x → 3 - 4x
x → 4x + 3
x → 4x + 5
25.
Find the circumference of a circle whose area is equal to 64 π cm2.
32 π cm
16 π cm
8 π cm
4 π cm
26.
Which of the following geometric figures is the plane shape of a cube?
Circle
Rectangle
Square
Triangle
27.
How many lines of symmetry has a rectangle?
4
3
2
1
28.
A rectangular box has length 20 cm, width 6 cm and height 4 cm. Find how many cubes of size 2 cm that will fit into the box.
120
60
30
15
29.
The interior angle of a regular polygon is 120o. How many sides has the polygon?
3
4
5
6
30.
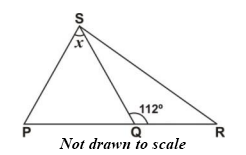
In the diagram above, length of PS = Length of SQ and angle SQR = 112o.
Find the value of x.
68o
56o
46o
44o
31.
XYZ is a right-angled triangle with length of sides as shown.
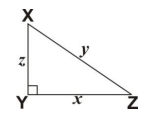
Which of the following equations gives the value of z2?
z2 = (x2 + y2)
z2 = (x - y)
z2 = (y2 - y2)
z2 = (x2 - y2)
32.
Express 7 min. 30 sec. as a percentage of 1 hour.
2.5%
7.5%
11.7%
12.5%
33.
The point (4, 5) is translated to the point (3, 1). What is the translation vector?
34.
In the diagram below, triangle QRT is the enlargement of QST.
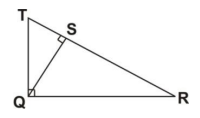
Which side of triangle QRT corresponds to side QT of triangle QST?
TS
TR
QR
SR
35.
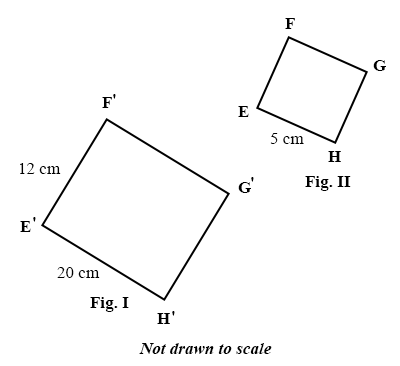
In the diagrams above Fig. I is an enlargement of Fig. II. Find the side EF of Fig. II.
20 cm
5 cm
4 cm
3 cm
36.
Express 4037 in standard form.
4.037 x 10-4
4.037 x 10-3
4.037 x 103
4.037 x 104
37.
Which of the following angles can be constructed by using the arcs at point C in the diagram below?
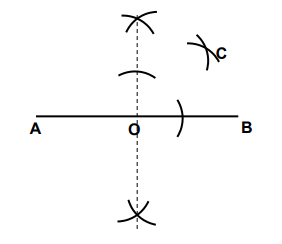
30o
45o
60o
75o
38.
Given that vector a = and b =
Find the value of x if a = b.
-2
-
2
39.
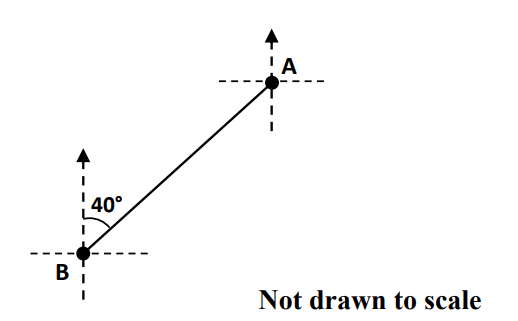
In the diagram above, the bearing of point B from A is
340o
220o
140o
50o
40.
Ama is 9 years older than Kwame. If Kwame is 18 years old, find the ratio of the age of Kwame to that of Ama.
3 : 2
1 : 3
2 : 3
2 : 1
(a)
Factorize (m + n)(2x - y)-x(m + n)
(b)
A and B are subsets of a universal set
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18} such that A = {even numbers} and B = {multiples of 3}.
(i)
List the elements of the sets A, B, (A ∩ B), (A ∪ B) and (A ∪ B)'.
(ii)
Illustrate the information in (i) on a Venn diagram.
(c)
Find the values of x and y in the vector equation:
+ 2 - = 0
(a)
Find the sum of 2,483.65, 701.532 and 102.7, giving your answer to one decimal place.
(b)
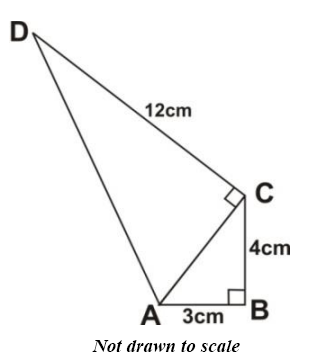
In the quadrilateral ABCD above, |AB|= 3 cm,|BC|= 4 cm, |CD|= 12 cm and angle ABC = 90o and angle ACD = 90o.
Calculate:
(i)
the perimeter of ABCD;
(ii)
the area of ABCD.
(a)
Evaluate , leaving your answer in standard form.
(b)
Kwame rode a bicyble for a distance of x km and walked for another hour at a rate of 6 km per hour. If Kwame covered a total distance of 10 km, find the distance x he covered by bicycle.
(c)
A rectangular tank of length 22 cm, width 9 cm and height 16 cm is filled with water. The water is poured into a cylindrical container of radius 6 cm. Calculate the
(i)
volume of the rectangular tank.
(ii)
depth of water in the cylindrical container.
[Take π = ]
(a)
Simplify: 7 - 4 + 2
(b)
The area of a trapezium is 31.5 cm2. If the parallel sides are of lengths 7.3 cm and 5.3 cm, calculate the perpendicular distance between them.
(c)
The marks scored by four students in a Mathematics test are as follows:
| Esi | - | 92 |
| Seth | - | 85 |
| Mary | - | 65 |
| Efe | - | x |
(i)
Write down an expression for the mean (average) of the marks.
(ii)
If the mean is less than 80, write a linear inequality for the information.
(iii)
Find the possible marks Efe scored in the test. Represent your answer on the number line.
(a)
Solve = + 2
(b)
Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular lines OX and OY on a graph sheet for the x-axis from -5 to 5 and the y-axis from -6 to 6.
(i)
Plot the points A(2, 3) and B(-3, 4) and join them with a long straight line.
(ii)
Plot on the same graph sheet, the points C(4, 2) and D(-2, -3) and join them with a long straight line to meet the line through AB.
(iii)
Measure the angle between the lines through AB and CD.
(iv)
Find the coordinates of the point at which the lines through AB and CD meet.
The following table shows the frequency distribution of the number of letters in the surnames of some students in a school.
| No. of letters | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| No. of students | 7 | 3 | 2 | 8 | 5 | 3 | 1 |
(a)
From the distribution, determine
(i)
the mode;
(ii)
the mean.
(b)
If a student is selected at random, find the probability that his/her name will contain more than 7 letters.
(c)
Draw a bar chart for the distribution.