1.
If P = {2,3,5,7} and Q = {2,4,6,8}, find P∩Q.
{2}
{3}
{4}
{5}
2.
Which of the following numbers is an integer?
-
-
0.5
1
3.
Find the Lowest Common Multiple (LCM) of 22 x 3 x 52 and 23 x 32 x 5.
22 x 3 x 5
22 x 32 x 52
23 x 3 x 5
23 x 32 x 52
4.
How many diagonals are in a rectangle?
1
2
3
4
5.
Simplify -4(3-5)+10-3(7+4)+30.
-1
15
56
65
6.
An iron rod 15 m long is divided into 12 equal parts. How long is each part?
0.80 m
1.25 m
1.50 m
3.00 m
7.
Convert 42 to a base two numeral.
1001010two
1010010two
1010100two
101010two
8.
Simplify
57
58
59
513
9.
A tank contains 400 litres of water. If 100 litres is used, what percentage is left?
25%
30%
40%
75%
10.
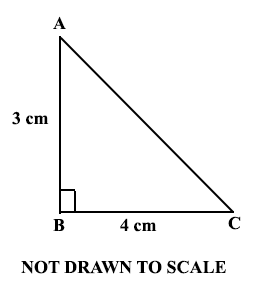
Triangle ABC is a right-angled triangle. Find the length of AC.
1 cm
5 cm
7 cm
12 cm
11.
Arrange the following fractions in descending order of magnitude:
,,,.
,,,
,,,
,,,
,,,
12.
Find the image of 3 under the mapping, x → 10 - 2x.
4
5
8
16
13.
Simplify + +
14.
If 2x = 5(x - 2) + 7, find the value of x.
-5
-1
1
5
15.
The table below shows the day and night temperatures of a town during a week. Use it to answer the question below.
| Week | Temperature (oC) | |
| Day | Night | |
| Monday | 33 | 24 |
| Tuesday | 29 | 25 |
| Wednesday | 32 | 23 |
| Thursday | 34 | 26 |
| Friday | 32 | 24 |
| Saturday | 30 | 24 |
| Sunday | 30 | 25 |
Find, correct to one decimal place, the average day temperature for the week.
24.4 oC
30.2 oC
31.4 oC
32.2 oC
16.
The table below shows the day and night temperatures of a town during a week. Use it to answer the question below.
| Week | Temperature (oC) | |
| Day | Night | |
| Monday | 33 | 24 |
| Tuesday | 29 | 25 |
| Wednesday | 32 | 23 |
| Thursday | 34 | 26 |
| Friday | 32 | 24 |
| Saturday | 30 | 24 |
| Sunday | 30 | 25 |
On which day was the change in temperature the least?
Monday
Saturday
Sunday
Tuesday
17.
A box contains 30 identical balls of which 16 are white and the rest yellow. If a girl picks a ball at random from the box, what is the probability that it is a yellow ball?
18.
Find the truth set of (x + 3) ≤ 2x - 1.
{x:x ≤ -3}
{x:x ≤ -1}
{x:x ≥ 1}
{x:x ≥ -3}
19.
The perimeter of the figure below is 71 cm. Find the diameter of the semi-circumference portion.
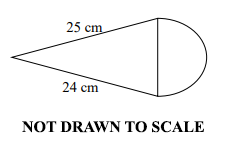
[Take π = ]
1.0 cm
3.5 cm
7.0 cm
14.0 cm
20.
Simplify - .
21.
Kojo is 20% heavier than Afua. If Kojo weighs 6 kg, what is Afua’s weight?
4.8 kg
5.0 kg
6.0 kg
7.2 kg
22.
Find the volume of a cylinder of height 3 cm and radius 2 cm.
6π cm3
12π cm3
18π cm3
24π cm3
23.
Given the points S(5, -2) and T(3, 2), calculate the gradient of the line ST.
-2
-
2
24.
Kofi invested GH₵ 150,000 at 2.5% per annum simple interest. How long will it take this amount to yield an interest of GH₵11,250.00?
2 years
3 years
4 years
5 years
25.
Express 3.75 as a mixed fraction.
3
3
3
3
26.
A map is drawn to the scale 1:100,000. What distance in kilometres is represented by 5 cm on the map?
0.5 km
5.0 km
50.0 km
500.0 km
27.
Given that r = and s = , find r - 2s.
28.
Esi went to the market and bought 500 g of meat, 850 g of fish and 900 g of eggs. What is the total weight of the items she bought in kilograms?
2.20 kg
2.25 kg
2.35 kg
22.50 kg
29.
A watch gains 1 minutes per hour. What is the total time gained from 12 noon to 12 midnight in a day?
9 minutes
15 minutes
18 minutes
36 minutes
30.
A printing machine prints 600 books in 3 hours. How many books will the machine print in 5 hours?
360 books
1000 books
1800 books
3000 books
31.
The bearing of Atoru from Busase is 275°. What is the bearing of Busase from Atoru?
180°
175°
095°
075°
32.
In a class of 24 pupils, 10 study French only and 8 study English only. If each pupil studies at least one of the two subjects, how many study English?
12
14
16
18
33.
Convert 84 to a base five numeral.
4130five
3014five
314five
114five
34.
In the diagrams below, triangle A1B1C1 is an enlargement of triangle ABC. Determine the scale factor.
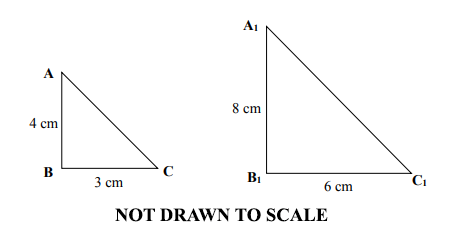
0.50
0.75
2.00
4.00
35.
Find the least number that must be added to 308 to make it divisible by 19.
4
7
15
18
36.
In a school of 940 pupils, the number of girls exceeds the number of boys by 150. How many girls are there in the school?
620
545
470
395
37.
Which of the following fractions is equivalent to ?
38.
(38)
In the diagram below, line PQ is parallel to RS and UV is a line drawn through PQ and RS.
Use the diagram to answer the question below.
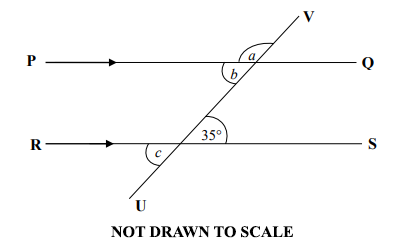
Find angle a.
35o
55o
135o
145o
39.
In the diagram below, line PQ is parallel to RS and UV is a line drawn through PQ and RS.
Use the diagram to answer the question below.

Angle b and angle c are
alternate angles.
vertically opposite angles.
corresponding angles.
interior opposite angles.
40.
Expand – x(3 – 2x).
-2x2 - 3x
2x2 - 3x
-2x2 + 3x
2x2 + 3x
(a)
Evaluate , leaving the answer in standard form.
(b)
An amount of GH₵4,200.00 was shared betwen Aba and Kwame. If Aba had of the amount,
(i)
how much did Kwame receive?
(ii)
what percentage of Aba's share did Kwame receive?
(c)
Find the value of x in the diagram below.
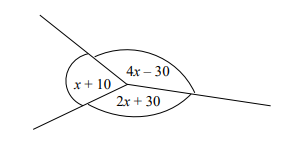
(a)
A car consumes a gallon of petrol for every 30 km drive. The driver of the car set out on a journey of 420 km with 10 gallons of petrol in the fuel tank.
(i)
How many more gallons of petrol will he need to complete the journey?
(ii)
Find the cost of the petrol used for the journey of 420 km if a gallon of petrol cost GH₵5.50.
(b)
The average number of spectators at a football competition for the first five days was 3,144. The attendance on the sixth day was 3,990. Find the
(i)
total attendance on the first five days
(ii)
average attendance for the 6 days.
(c)
The area enclosed by a square garden is 121 m2. What is the distance around the garden?
(a)
The table shows the number of students who scored more than 80% in the listed subject.
| Subject | Number of students |
| Biology | 26 |
| Physics | 30 |
| Chemistry | 32 |
| French | 38 |
| Geography | 24 |
| History | 30 |
(i)
Draw a pie chart for the distribution.
(ii)
What is the probability that a student chosen at random from the distribution, offers Chemistry?
(b)
A woman bought 210 oranges for GH₵7.50. She sold all of them at 3 for 15 Gp. Find the
(i)
total selling price of the oranges;
(ii)
percentage profit.
The marks scored by some students in a Mathematics test are as follows:
| 3 | 3 | 5 | 6 | 3 | 4 |
| 7 | 8 | 3 | 4 | 5 | 4 |
| 7 | 4 | 3 | 7 | 4 | 6 |
| 4 | 8 | 4 | 5 | 6 | 3 |
| 8 | 4 | 5 | 6 | 4 | 5 |
(a)
Construct a frequency distribution table for the scores.
(b)
Using the table, find for the distribution, the
(i)
mode;
(ii)
mean, correct to one decimal place;
(iii)
median.
(a)
(i)
Find the least Common Multiple (L.C.M.) of 9, 18 and 16.
(ii)
Arrange , and in ascending order of magnitude.
(b)
Using a ruler and a pair of compass only,
(i)
construct a triangle PQR with length PQ = 10 cm, angles QPR = 45o and PQR = 60o.
(ii)
Construct the perpendicular bisectors of PR and RQ to meet at T.
(iii)
Measure the length of TP.
(i)
Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes Ox and Oy on a graph sheet.
(ii)
Mark on the same graph sheet, the x-axis from -5 to 5 and y-axis from -6 to 6.
(iii)
Plot the points P(4, 2), Q(2, 5) and R(2, 2). Join the points P, Q, R to form a triangle PQR
(iv)
Using the x-axis as a mirror line, draw the image P1Q1R1 of the triangle PQR such that P→P1, Q→Q1, R→R1
(v)
Write down the coordinates of P1, Q1 and R1.
(vi)
Translate triangle PQR by the vector such that P→P2, Q→Q2, R→R2
(vii)
Label the vertices of triangle P2Q2R2