1.
If A = {5,10,15,20,25,125} and B = {5,10,15,20,25,625}, list the elements of A ∪ B
{5,25}
{10,20,125,625}
{5,15,25,125,625}
{5,10,15,20,25,125,625}
2.
Express 1.25 as a percentage.
25%
75%
125%
175%
3.
Arrange the following in ascending order of magnitude:
0.301,0.3,0.33,0.03.
0.03,0.3,0.301,0.33
0.03,0.301,0.3,0.33
0.33,0.3,0.301,0.03
0.33,0.301,0.3,0.03
4.
Evaluate 53 - (-7) + (-15).
31
45
61
75
5.
Given that A = {a, e, i, o, u} and B = {r, s, t}, how many elements are in A∩B?
0
1
2
3
6.
Convert 2114five to a base ten numeral.
194
280
284
300
7.
Simplify .
8.
A car uses 150 litres of petrol in 45 mins. How many litres of petrol will it use in 1 hour?
375 litres
230 litres
225 litres
200 litres
9.
Simplify .
10.
Find the rule of the mapping:
| 1 | 2 | 3 | 4 | 5 | x |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| 5 | 8 | 11 | 14 | 17 | y |
x + 2
x + 4
2x + 3
3x + 2
11.
Given that –1 = 2 – m, find m
- 3
- 1
1
3
12.
The perimeter of a rectangle is 48 cm. if the length is 14 cm, find its width.
24 cm
20 cm
10 cm
3.4 cm
13.
Make d the subject of the relation n = 2d + 3
d =
d =
d =
d =
14.
Calculate the gradient of the straight line joining the points A(3,5) and B(–2,3).
-
-
15.
Use the diagram below to answer the question below.
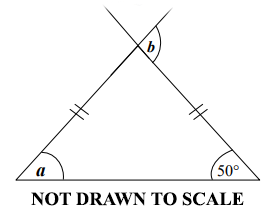
Find the angle marked a.
70o
50o
40o
30o
16.
Use the diagram below to answer the question below.

Find the angle marked b.
150o
140o
110o
100o
17.
If S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, find the probability that a number selected at random from S is odd.
18.
Find the vector which translates the point (4, –5) to (3, –2)
19.
Factorize completely the expression 2xy – 6y + 7x – 21
(x – 3)(2y + 7)
(x + 3)(2y – 7)
(y – 3) (2x +7)
(y + 3) (2x – 7)
20.
The area of a circle is 154 cm2. Find the diameter.
(Take π = )
7 cm
14 cm
21 cm
49 cm
21.
Mame Esi rides her bicycle to school and back everyday. If the distance from her home to the school is 2345 m, how many kilometers does she cover everyday?
4.98 km
4.69 km
3.96 km
3.68 km
22.
The length of a rectangular fence is 25 m. The ratio of the length to the width is 5:3. Find the width of the rectangular fence.
9 m
13 m
15 m
16 m
23.
Evaluate - b, if a = 30 and b = 1.
-1
-
1
24.
How many 15Gp Christmas cards can be bought with GH₵18.00?
120
150
180
270
25.
If u = and v = , find u + v.
26.
If 4956 × 25 = 123,900, evaluate 495.6 × 2.5 leaving the answer in standard form.
1.239 × 102
1.239 × 103
1.239 × 104
1.239 × 105
27.
Which of the following expressions is illustrated on the number line.
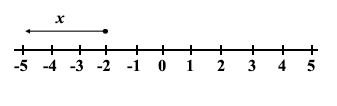
x ≤ -2
x < -2
x ≥ -2
x > -2
28.
If 180 oranges were shared among Kwame and Ama in the ratio 7:5, respectively, how many oranges did Ama receive?
45
60
75
90
29.
Calculate the simple interest on GH₵450.00 for 2 years at 12% per annum.
GH₵ 191.00
GH₵ 108.00
GH₵ 54.00
GH₵ 27.00
30.
If 15% of the length of a rope is 75 cm, find half of the length of the rope.
500 cm
250 cm
150 cm
100 cm
31.
In an office, of the telephone bill is paid by Tom, by Azuma and the remaining by Tina. What fraction is paid by Tina?
32.
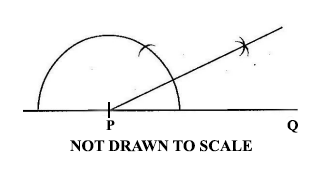
Which of the following best describes the construction?
Constructing a perpendicular at P
Constructing the bisector of line PQ
Constructing an angle of 30o at P
Constructing an angle of 45o at P
33.
Express 0.055 as a common fraction
34.
The table below shows the distribution of workers in some trades.
| Trade | Shoe making | Mining | Road transport | Agriculture | Manufacturing goods |
| Number of workers | 300,000 | 25,000 | 160,000 | 225,000 | 165,000 |
Use this information to answer the question below.
Which trade employed the most number of workers?
Agriculture
Manufacturing
Shoe making
Road transport
35.
The table below shows the distribution of workers in some trades.
| Trade | Shoe making | Mining | Road transport | Agriculture | Manufacturing goods |
| Number of workers | 300,000 | 25,000 | 160,000 | 225,000 | 165,000 |
Use this information to answer the question below.
How many people are employed under all the trade?
325,000
485,000
650,000
875,000
36.
Aba bought a carton of fish at GHC 80.00 and sold it at a profit of GHC 13.60. Find the selling price.
GH₵ 66.40
GH₵ 93.60
GH₵ 103.60
GH₵ 144.00
37.
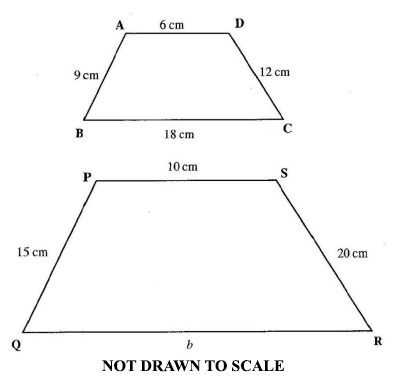
If the two figures ABCD and PQRS are similar, find the value of b.
60 cm
40 cm
33 cm
30 cm
38.
A man shared an amount of money between his two children, Esi and Ato in the ratio 2:3 respectively. If Ato received GH₵ 45.00, what was the total amount shared?
GH₵ 18.00
GH₵ 27.50
GH₵ 75.00
GH₵ 112.50
39.
How many edges has a cuboid?
16
12
8
4
40.
Two sets whose intersection is an empty set are
disjoint sets.
equivalent sets.
finite sets.
empty sets.
(a)
Fifty students in a class took an examination in French and Mathematics. If 14 of them passed French only, 23 passed in both French and Mathematics and 5 of them failed in both subjects, find
(i)
the number of students who passed in French
(ii)
the probability of selecting a student who passed in Mathematics
(b)
Solve the inequality 2x −1 ≥ 5x −6
(a)
Convert 444five to a base two numeral.
(b)
A man had three GH₵50.00, seven GH₵20.00 and five GH₵10.00 notes in his pocket. If he bought a bicycle for GH₵150.00 and two mobile phones at GH₵80.00 each, how many GH₵20.00 and GH₵10.00 notes did he have left?
(a)
Using a ruler and a pair of compasses only,
(i)
construct a triangle XYZ with length XY = 7 cm, length YZ = 5 cm and angle XYZ = 45o.
(ii)
Measure and write down the length of XZ.
(b)
Given that the circumference of a circle is 44 cm, find
(i)
the radius of the circle;
(ii)
the area of the circle.
[Take π = ]
The table shows the distribution of marks of students in a class test.
| Mark | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency | 5 | 6 | 5 | 3 | 4 | 2 |
(a)
Using a graph sheet, draw a bar chart for the distribution.
(b)
Calculate the mean mark of the distribution correct to the nearest whole number.
(a)
Simplify 6.
(b)
Copy and complete the magic square so that the sum of numbers in each row or column or diagonal is 18.
| 4 | ||
| 7 | 8 |
(c)
Find the sum of all the factors of 24.
(d)
Given that m = , n = and r =
Find m + n + r.
(a)
Copy and complete the table for the relation y = 2x + 5.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -1 | 1 | 5 | 13 |
(b)
(i)
Using a scale of 2 cm to 2 units on both axes, draw two perpendicular axes 0x and 0y on a graph sheet.
(ii)
Mark the x-axis from -6 to 10 and y-axis from -6 to 14.
(iii)
Using the table, plot all the points of the relation y = 2x + 5 on the graph.
(iv)
Draw a straight line through the points.
(c)
Use the graph to find
(i)
y when x = 1.6
(ii)
x when y = 10