1.
Which of the following is a finite set?
{2,4,6,8,...}
{1,2,3,4,...}
{...,2,3,5,7}
{3,6,9,12}
2.
Given that M={a,b,c} find the number of subsets of M
3
4
6
8
3.
If P = {2,3,4,6,8} and Q = {1,2,3,4}, find P∩Q.
{2,3,4}
{7,9,10}
{2,3,4,6,8}
{1,2,3,4,6,8}
4.
A boy bought 3 pairs of socks at GH₵17.50 per a pair and paid with two GH₵50.00 notes. How much change was he given?
GH₵27.50
GH₵37.50
GH₵47.50
GH₵48.50
5.
Find the Least Common Multiple (LCM) of the numbers 5,10 and 12.
2 x 3 x 5
2 x 32 x 5
22 x 3 x 5
22 x 32 x 52
6.
Correct 48,947.2547 to the nearest hundred.
490
48,900
48,950
49,000
7.
Simplify: 16 + 5.6 + 0.681
2.2281
22.281
222.81
2228.1
8.
Evaluate - +
9.
Arrange the following integers from the least to the highest -4,9,-10,-7,and 2.
-10,-7,-4,2,9
-10,9,-7,-4,2
-4,-7,-10,2,9
2,-4,-7,9,-10
10.
Simplify: (46 x 102) + (102 x 54)
1,020
10,200
102,000
1,020,000
11.
Correct 5178.3426 to two decimal places.
5178.00
5178.30
5178.34
5178.35
12.
Find the simple interest on GH₵120,000.00 for 5 months at 12% per annum.
GH₵6,000.00
GH₵7,200.00
GH₵50,000.00
GH₵72,000.00
13.
Fifteen boys took 12 hours to weed a plot of land. If nine boys work at the same rate, how long will it take them to weed the plot of land?
6 hours
7
11
20 hours
14.
A car costs GH₵12,500.00. A discount of 9% is given for cash payment. Find the cost of the car when payment is made by cash.
GH₵10,250.00
GH₵11,250.00
GH₵11,375.00
GH₵13,625.00
15.
Simplify:52 x 22 x 52 x 2
22 x 52
22 x 54
23 x 52
23 x 54
16.
The table shows the marks of some students in a test. Use the information to answer the question below.
| Marks | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Number of students | 3 | 4 | 5 | 4 | 5 | 4 | 7 | 3 | 4 | 2 | 2 |
What is the modal mark?
2
5
6
10
17.
The table shows the marks of some students in a test. Use the information to answer the question below.
| Marks | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Number of students | 3 | 4 | 5 | 4 | 5 | 4 | 7 | 3 | 4 | 2 | 2 |
How many students failed the test, if the pass mark was 4?
4
6
16
21
18.
What is the probability of obtaining 4, when a fair die is tossed once?
19.
Make P the subject of the relation, R =
P = Q - 2R
P = 2R - Q
P = 2R + Q
P = 2Q + R
20.
Given that t = p2 + 1, find p when t = 10.
3.0
4.5
11.0
81.0
21.
Simplify: 4(x + 2)-3(x +1).
x + 5
x + 11
7x + 5
7x + 11
22.
When a number is doubled and the result is decreased by 9, the answer is 19. Find the number.
5
7
14
16
23.
Solve the inequality 2x + 10 ≥ x - 5.
x ≥ 10
x ≤ 10
x ≤ 40
x ≥ 40
24.
Find the image of 5, under the mapping x → 4x - 7.
3
13
20
27
25.
An angle which is greater than 180o but less than 360o is
a right angle.
an acute angle.
an obtuse angle.
a reflex angle.
26.
How many lines of symmetry has a rectangle?
1
2
3
4
27.
The perimeter of an isosceles triangle is 45 cm. Find the length of the third side, if each of the equal sizes is 14 cm long.
11 cm
14 cm
17 cm
31 cm
28.
Find the area of a circle whose diameter is 7 cm.
[Take π = ]
11 cm2
38 cm2
44 cm2
54 cm2
29.
The mean of three number is 12. If two of the numbers are 14 and 16, find the third number.
6
12
30
36
30.
The sum of the interior angles of a regular polygon is 540o. Find the number of sides of the polygon.
7
6
5
4
31.
The figure QPR is an equilateral triangle. If angle PRS = (2x - 10)o, find the value of x.
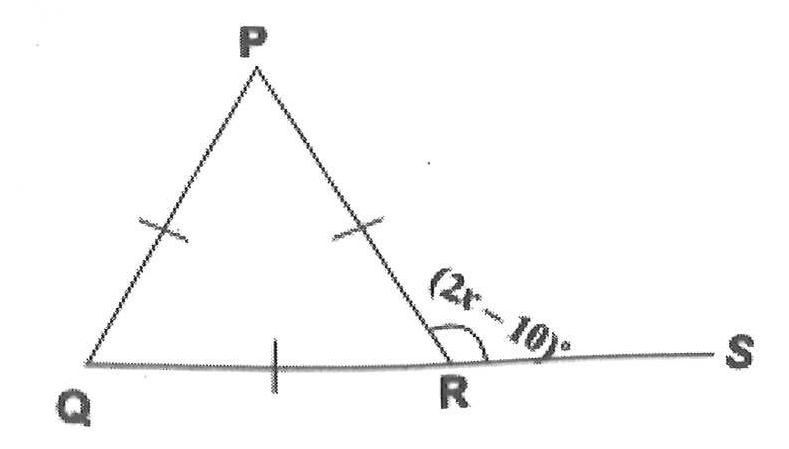
55
65
85
95
32.
The diagonal of a rectangle is 10 cm long. If the length of the rectangle is 8cm, find its breadth.
2 cm
3 cm
5 cm
6 cm
33.
In an enlargement, XY → X1Y1.
If |XY| = 24 cm and |X1Y1| = 8 cm, calculate the scale factor of the enlargement.
34.
Study the triangle of odd numbers and use it to answer the question below.
| 13 | b | c | 19 | |||
| 7 | 9 | a | ||||
| 3 | 5 | |||||
| 1 |
Evaluate: 13 + b + c + 19.
62
64
74
76
35.
Study the triangle of odd numbers and use it to answer the question below.
| 13 | b | c | 19 | |||
| 7 | 9 | a | ||||
| 3 | 5 | |||||
| 1 |
Evaluate: a + b + c
24
29
36
43
36.
Simplify +
37.
The bearing of X from Y is 196o. What is the bearing of Y from X?
016o
074o
106o
244o
38.
If a = -4 and b = 3, evaluate .
1
-
39.
The point P(-3,7) is reflected in the x-axis. Find its image.
(-3,-7)
(-3,7)
(-7,3)
(3,-7)
40.
The instrument used to measure the angle between two lines that meet at a point is known as a
pair of compasses.
set-square.
protractor.
pair of dividers.
(a)
In an examination, 50 candiates sat for either Mathematics or English Language.
60% passed in Mathematics and 48% passed in English Language. If each candiate passed in at least one of the subjects, how many candidates passed in:
(i)
Mathematics?
(ii)
English Language?
(b)
Illustrate the information given in (a) on a Venn diagram.
(c)
Using the Venn diagram, find the number of candidates who passed in:
(i)
both subjects;
(ii)
Mathematics only.
(d)
If a = and b = are equal vectors, find the values of x and y.
(a)
The cost (P), in Ghana cedis, of producing n items is given by the formula,
P = n + 1800.
Find the:
(i)
cost of producing 2,000 items;
(ii)
number of items that will be produced with GH₵2,400.00;
(iii)
cost when no items are produced.
(b)
A passenger travelling by air is allowed a maximum of 20 kg luggage. A man has four bags weighing 3.5 kg, 15 kg, 2 kg and 1.5 kg.
(i)
Find the excess weight of his luggage.
(ii)
Express the excess weight as a percentage of the maximum weight allowed.
(a)
A doctor treated 2,000 patients over a period of time. If he worked for 5 hours a day and spend 15 minutes on each patient, how many days did the doctor spend to treat all the patients?
(b)
The pie chart shows the distribution of textbooks to six classes A,B,C,D,E and F in a school.
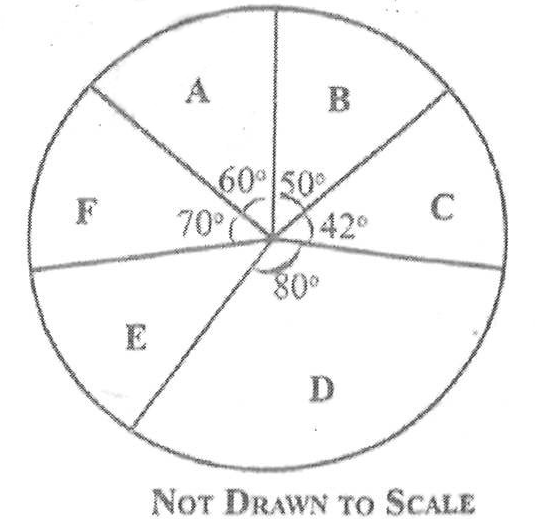
(i)
If class D was given 720 textbooks, how many textbooks were distributed to each of the remaining classes?
(ii)
What is the average number of textbooks distributed to the classes?
(iii)
How many classes had less than the average number of textbooks distributed?
(a)
Using a scale of 2 cm to 1 unit on both axes, draw on a graph sheet two perpendicular axes 0x and 0y for -5 ≤ x ≤ 5 and -5 ≤ y ≤ 5.
(i)
Plot, indicating the coordinates of all points P(1,1), Q(1,2),R(2,2) and S(2,1) on the graph sheet. Join the points to form square PQRS.
(ii)
Draw and indicate clearly all coordinates, the image P1Q1R1S1 of square PQRS under an enlargement from the origin with a scale factor of 2, where P → P1,Q → Q1, R → R1 and S → S1.
(iii)
Draw and indicate clearly all coordinates, the image P2Q2R2S2 of square P1Q1R1S1 under a reflection in the x-axis where P1 → P2,Q1 → Q2, R1 → R2 and S1 → S2.
(b)
Using the graph in (a), find the gradient of line R2S.
(a)
Given that u = 4, t = 5, a = 10 and s = ut + at2, find the value of s.
(b)
The selling price of a gas cooker is GH₵450.00. If a customer is allowed a discount of 20%, calculate the:
(i)
discount;
(ii)
amount paid by the customer.
(c)
A crate of minerals containing ten bottles of Coca Cola and fourteen bottles of Fanta was given to some children for a birthday party. If a child chose a drink at random from the crate, find the probability that it was Fanta.
(a)
Using a ruler and a pair of compasses only, construct:
(i)
triangle XYZ with |XY| = 9 cm,
|YZ| = 12 cm and |XZ| = 8 cm.
(ii)
the perpendicular bisector of line XY.
(iii)
the perpendicular bisector of line XZ.
(b)
(i)
Label the point of intersection of the two bisectors as T;
(ii)
With point T as center, draw a circle of radius 6 cm.
(c)
Measure:
(i)
|TX|;
(ii)
angle XYZ.