1.
Two brands of air conditioners S and T cost GH₵ 3,000.00 and GH₵ 4,000.00 respectively. A company budgeted GH₵ 20,000.00 to buy air conditioners. If the company bought 5 units of brand S instead of brand T, how much did it save?
GH₵ 1,000.00
GH₵ 5,000.00
GH₵ 20,000.00
GH₵ 15,000.00
2.
Zalia and Amina shared an amount of money in the ratio 2 : 5. If Amina had GH₵ 150.00 more than Zalia, how much did they share?
GH₵ 100.00
GH₵ 250.00
GH₵ 450.00
GH₵ 350.00
3.
Which of the following is an example of quantitative data?
Colour
Gender
Marital status
Length
4.
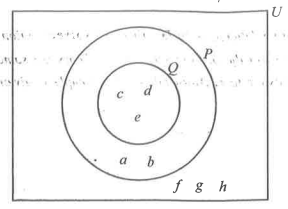
In the diagram, P and Q are two sets and U is the universal set.
Use the information to answer the question below
Find P ∩ Q.
{c, d, e}
{a, b}
{c, b, c, d, e}
{f, g, h}
5.

In the diagram, P and Q are two sets and U is the universal set.
Use the information to answer the question below
How many members are in set Q
2
3
8
5
6.
Amadu walked to a point such that he is always the same distance from two villages P and Q.
Which of the following best describes the locus of Amadu?
An arc passing through line PQ
A circle passing through line PQ
Straight line PQ
Perpendicular bisector of line PQ
7.
A bag of rice weighs 2 kg. If the empty bag weights 150 g, find the weight of the rice.
[1 kg = 1,000 g]
0.175 kg
0.185 kg
1.850 kg
1.750 kg
8.
Andrews drew three lines such that the length of the first one is 10 cm, the second is 15 cm longer than the first one and the third is 9 cm less than the second. Find the length of the third line.
4 cm
14 cm
34 cm
16 cm
9.
Find the truth set of 2x - 4 < 6 + 3x.
{x : x < 2}
{x : x > -2}
{x : x > -10}
{x : x < 10}
10.
The locus of points equidistant from a fixed point is called a
chord.
circle.
mediator.
diameter.
11.
Evaluate: + - .
2 - 3
2 + 3
5
12.
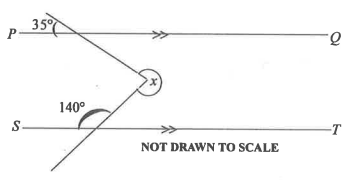
In the diagram, line PQ is parallel to line ST. Find the value of the angle marked x.
140°
220°
290°
285°
13.
A hawker is carrying a basket load of three types of fruits: oranges, mangoes and pears.
If of the fruits are oranges and mangoes, what percentage of the fruits are pears?
9 %
18 %
64 %
36 %
14.
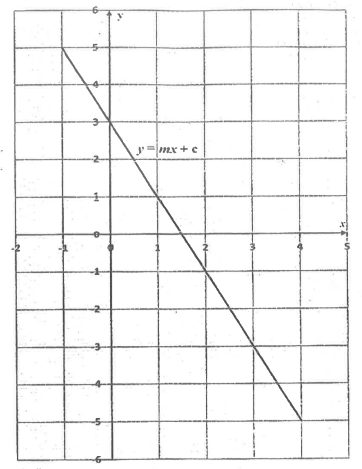
The diagram shows the graph of a linear relation of the form y = mx + c.
Use the graph to answer the question below
Find the slope of the relation.
-2
-1
2
1
15.

The diagram shows the graph of a linear relation of the form y = mx + c.
Use the graph to answer the question below
Find the equation of the relation.
y = -2x + 3
y = -2x + 2
y = 2x + 3
y = 2x - 3
16.
Araba is 3 years younger than her sister. If the sum of their ages is 17 years, find Araba's age.
7 years
8 years
10 years
9 years
17.
A number of oranges are shared among 50 students and each got 15 oranges. If the same number of oranges are shared equally among 30 students, how many will each student get?
13
15
25
20
18.
If the bearing of Q from P is 120°, find the bearing of P from Q.
060°
210°
300°
240°
19.
Given the vectors m = and n = , find 2m + n.
20.
Simplify:
32m
32m - 1
32m + 2
32m + 1
21.
There are 15 white and 25 black identical balls in a box. If a ball is selected at random from the box, find the probability that it is white.
22.
The area of a rectangle is 18 cm2. If the width is 2 cm, find its perimeter.
18 cm
20 cm
36 cm
22 cm
23.
Find the interest on GH₵ 400.00 for 2 years at 10% simple interest per annum.
GH₵ 8.00
GH₵ 40.00
GH₵ 80.00
GH₵ 60.00
24.
One of the factors of the expression 4m2 + 12m - 8m - 24 is (4m - 8). Find the other factor.
m - 3
m + 3
2m + 3
2m - 3
25.
An article which cost GH₵ 600.00 was sold at a discount of 10%. Find the selling price.
GH₵ 60.00
GH₵ 504.00
GH₵ 560.00
GH₵ 540.00
26.
Make m the subject of the relation = + .
m =
m =
m =
m =
27.
The point P(-2, 3) is translated by a vector to a point R. Find the coordinates R.
(6, -2)
(-3, 6)
(-3, -6)
(-1, 0)
28.
A frog leaps in such a way that its distance, in metres, from its starting position after each leap is given by 4, 7, 10, ...
Find its distance from the starting position after the 10th leap.
28
31
37
34
29.
A bus departed from Elmina at 9:15 pm and arrived in Accra at 2:45 am the next day.
How long did the journey take?
4 hours 20 minutes
4 hours 30 minutes
5 hours 30 minutes
5 hours 20 minutes
30.
Simplify: 3x - 2(3 + 2x) + x(2x + 4).
2x2 + 11x - 6
2x2 + 3x - 6
2x2 - 4x - 6
2x2 + 4x - 6
31.
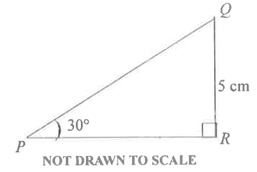
In the diagram, ∠ QPR = 30° and |QR| = 5 cm.
[Take sin 30° = ].
Find the length of PQ.
2.5 cm
5.0 cm
12.0 cm
10.0 cm
32.
A fair coin and a fair die are rolled together once. Find the probability of obtaining a tail and an odd number.
33.
If the gradient of a straight line is zero, then the line
is vertical.
is horizontal.
falls to the right.
rises to the right.
34.
Madam Nancy wants to know which of the teachers in her school is liked best by most of the students. Which of the following methods is most suitable for collecting the data?
Experiment
Database
Questionnaire
Observation
35.
Mensah packed 1,800 apples into a number of boxes. If each box contained 120 apples, how many boxes were fully packed?
15
16
18
17
36.
The cost of three items at a shop are GH₵ 72.00, GH₵ 1,105.00 and GH₵ 216.00.
If a customer bought all the three items and received a change of GH₵ 107.00, how much did he initially give the shopkeeper?
GH₵ 1,300.00
GH₵ 1,400.00
GH₵ 2,000.00
GH₵ 1,500.00
37.
| Number on die | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency | 4 | 3 | 3 | 2 | 3 | 5 |
The table shows the results when a student tossed a die many times.
Use the information to answer the question below
Find the mode.
6
5
3
4
38.
| Number on die | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency | 4 | 3 | 3 | 2 | 3 | 5 |
The table shows the results when a student tossed a die many times.
Use the information to answer the question below
How many times did the student throw the die?
6
18
21
20
39.
Find the image of the point (-3, 5) when it is rotated through 360° about the origin.
(5, -3)
(-3, 5)
(-5, 3)
(-3, -5)
40.
A story book contains 50 pages. If a student reads 10 pages per hour, find the relationship between the number of unread pages (N) and time (t).
N = 10t + 50
N = -10t + 50
N = -t + 5
N = 10t - 50
(a)
A fair die and a fair coin are thrown together once.
(i)
Write down the set of all possible outcomes.
(ii)
Find the probability of obtaining a prime number and a tail.
(b)
The map of a field is drawn to a scale of 1 : 100. If the width and area of the field on the map are 8 cm and 88 cm2 respectively, find in m2, the area of the actual field.
(c)
Copy and complete the 3 x 3 magic square such that the sum of the numbers in each row, column and diagonal is equal to 21.
| 10 | 3 | |
| 7 | ||
(a)
Given the vectors p = , q = and p = q, find the values of m and n.
(b)
A man shared an amount of money between his children Baaba and William in the ratio 6 : 5. Baaba received GH₵ 1,200.00
(i)
find the total amount shared.
(ii)
William invested his share in an account at the rate of 20% simple interest per annum for 2 years. Find the total amount in his account at the end of the 2 years.
(a)
Simply: 3 + 2 - +
(b)
A wire of length 38 cm is bent into the shape of a rectangle whose length is 7 cm more than the width.
Find the area of the rectangle.
(c)
If 15% of the length of a rope is 720 metres, find half of the length of the rope.
(a)
Using a ruler and a pair of compasses only, construct ∆PQR such that angle PQR = 90°, |PQ| = 5.5 cm and |QR| = 8 cm.
(b)
Construct a perpendicular of PR from Q.
(c)
Locate M, the intersection of the perpendicular and PR.
(d)
Measure:
(i)
|MR|;
(ii)
|QM|.
(e)
Calculate, correct to the nearest whole number, the area of triangle QMR.
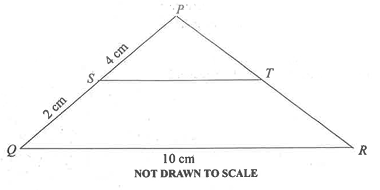
(a)
In the diagram, ∆PQR is an enlargement of ∆PST. |PS| = 4 cm, |QS| = 2 cm and |QR| = 10 cm.
(i)
Find the length of ST.
(ii)
If |PQ| = |PR|, find the area of ∆PQR
(b)
The total area of a school compound is 900m2. The school has Administration and Classroom block, Library, School Park, Roads and Walkways.
The areas of the Administration and Classroom block, Library and School Park are 300m2, 200m2 and 120m2 respectively.
Find the area covered by Roads and Walkways altogether.
(a)
Copy and complete the table for the relation F = C + 32.
Where F and C are degrees Fahrenheit and degrees Celsius respectively.
| °C | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| °F | 32 | 68 |
(b)
Using a scale of 2 cm to 10 units on the vertical axis (°F) and 2 cm to 5 units on the horizontal axis (°C), draw a linear graph for the relation.
(c)
Use the graph to find the temperature in degrees celsius when F = 55 degrees.
(d)
Interpret the slope of the relation.