1.
Which of these is the equation of a straight line?
Circle your answer.
y = 6x2
y = x – 6
y = x2 + 6
y =
2.
What is 0.28 as a fraction of 0.8?
Circle your answer.
3.
Circle the calculation that increases 240 by 7.5%
240 × 1.0705
240 × 1.705
240 × 1.075
240 × 1.75
4.
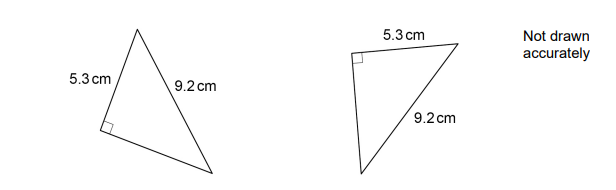
Circle the reason why the triangles are congruent.
ASA
RHS
SAS
SSS
5.
Work out 80 000 000 ÷ 200
Give your answer in standard form.
Answer: ...................................................................
6.
Work out
Give your answer as a whole number.
Answer: ...................................................................
7.
Simplify 8 × 26 × 24
Give your answer as a power of 2
Answer: ...................................................................
8.
In a group of 98 students
25 study both Art and French
10 study Art but do not study French
41 study French.
Joel draws this Venn diagram to represent the information.
ξ = the group of 98 students
A = the students who study Art
F = the students who study French
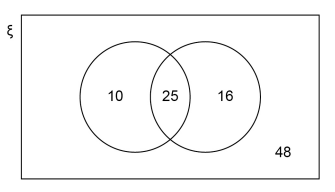
Make two criticisms of his diagram.
Criticism 1:
Criticism 2:
9.
In a week, Samir is paid
a basic hourly rate for the first 30 hours worked
an overtime hourly rate for any extra hours worked.
The graph shows his pay for working up to 40 hours in a week.
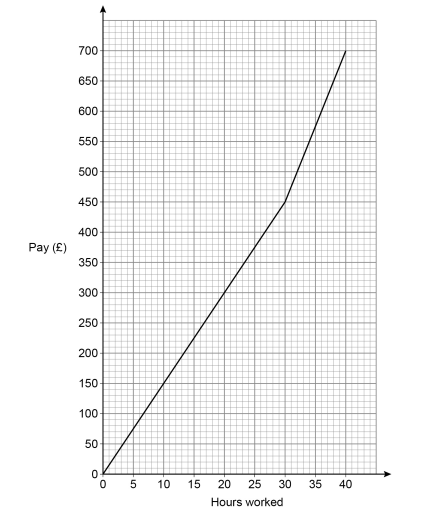
Work out the ratio basic hourly rate : overtime hourly rate
Give your answer in its simplest form.
Answer: :
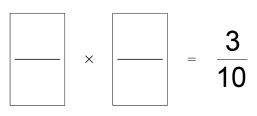
10.
In each box, write a fraction less than 1 to make a correct calculation.
11.
In each box, write a decimal less than 1 to make a correct calculation.

12.
Use a ruler and compasses in this question.
ABCD represents a garden.
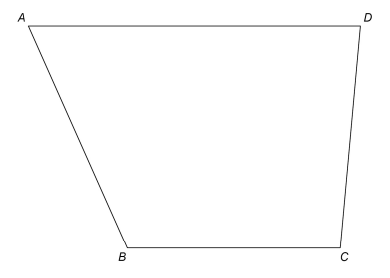
A tree is to be planted in the garden.
The tree will be in the region that is closer to AB than to BC.
Label the region, R, where the tree could be planted.
Show all your construction lines.
13.
Here are two shapes, P and Q.
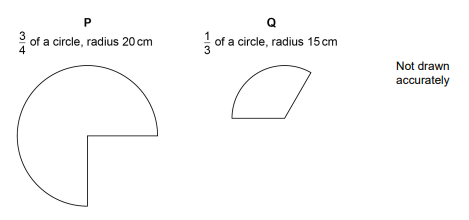
How many times bigger is the area of P than the area of Q?
You must show your working.
Answer: ...................................................................
14.
In a game, two bags, A and B, contain cards.
Each card is marked Yes or No.
The table shows the number of each type of card in the bags.
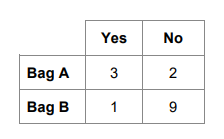
In the game, a player picks one card at random from each bag.
The cards are then put back into the bags.
a)
Complete the tree diagram.
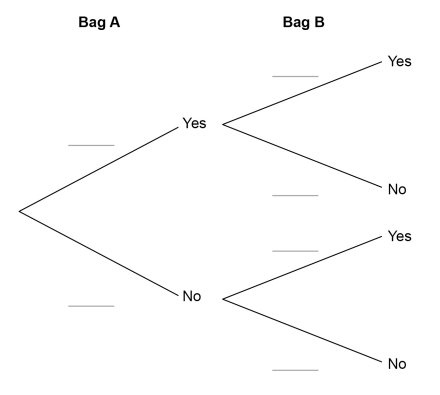
b)
To win a prize, a player must pick two cards marked Yes.
450 people each play the game once.
How many people are expected to win a prize?
Answer: ...................................................................
15.
Solve =
w = ...................................................................
16.
15 workers can complete a job in 8 days.
How many more workers are needed to complete the job in 6 days?
Assume that all of the workers work at the same rate.
Answer: ...................................................................
17.
The cross section of a prism has n sides.
Circle the expression for the number of faces of the prism.
n
2n
3n
n + 2
18.
Circle the letter of the possible sketch graph of y = x3 – 4
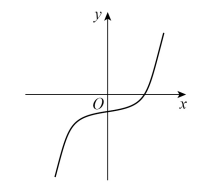
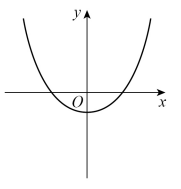
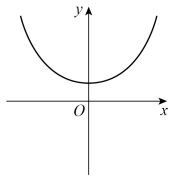
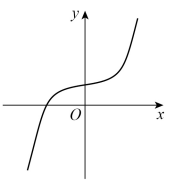
19.
75 people attend a clinic.
Their ages are recorded and a cumulative frequency diagram is drawn.
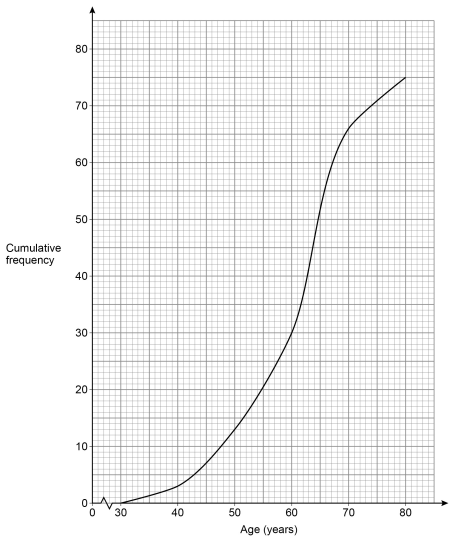
A nurse makes a statement about the ages of the people at the clinic.
He says,
"More than twice as many people are in their 60s as in their 50s."
Is he correct?
Tick a box.
Show working to support your answer.
Yes
No
20.
12x3 + 7x2 + 3x – 10 ≡ 2(ax3 + x2 + 2x – 5) + x(bx + c)
Work out the values of a, b and c.
a = b = c =
21.
The first three terms of a sequence are x y xy
The sequence is continued by multiplying the previous two terms.
Circle the 5th term of the sequence.
x3y3
x5y5
x3y4
x2y3
22.
The first three terms of a sequence are x y xy
The sequence is continued by multiplying the previous two terms.
The 8th term of the sequence is x8y13
The value of this term is negative.
What does this mean about the values of x and y?
Tick one box for each row.
| Must be positive | Must be negative | Could be either | Mark | |
| x | ||||
| y |
23.
Rearrange y = to make x the subject.
Answer: ...................................................................
24.
Five points are connected by vectors.
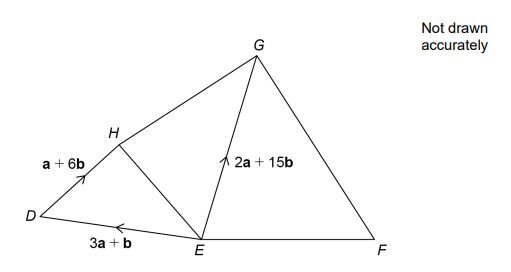
FG→ = 2EH→
Work out FE→ in terms of a and b.
Answer: ...................................................................
25.
Work out 0.68. - 0.45.
Give your answer as a fraction in its simplest form.
Answer: ...................................................................
26.
On the grid, identify the region represented by
x > 3 and y > 1 and x + y ≤ 7
Label the region R.
27.
Simplify fully -
Answer: ...................................................................
28.
Simplify fully (y2 – 3y) ×
Answer: ...................................................................
29.
Here is the speed-time graph for a 50-second journey.
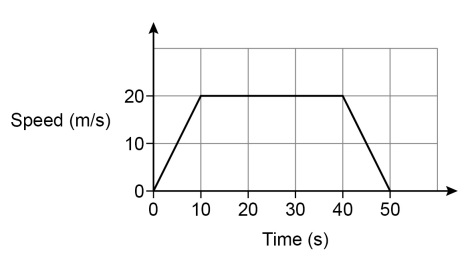
Circle the acceleration, in m/s2, halfway through the journey.
0
2
20
25
30.
Here is the speed-time graph for a 50-second journey.

Work out the total distance travelled.
Answer: .................................................................. m
31.
Zoe and Amy are playing a board game.
• They each have one disc and take turns to roll a fair, ordinary dice.
• The player moves their disc clockwise the number of spaces shown on the dice.
• The winner is the first player whose disc is on HOME at the end of a turn.
Here is the board after Amy's turn.
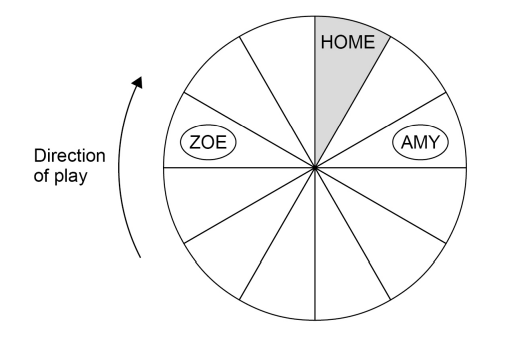
Work out the probability that Zoe wins within her next two turns.
Answer: ...................................................................
32.
The grid shows the graph of y = f(x).
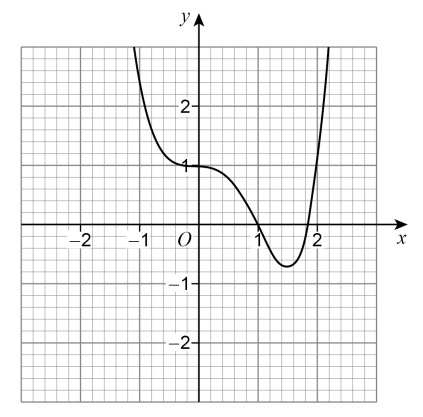
On the grid, draw the graph of y = –f(x)
33.
Work out the value of (cos 30° × sin 45° × tan 60°)2
Answer: ...................................................................