1.
If set A = {1, 2, 3, 4, 5,…} is given, then it represents:
Whole numbers
Rational Numbers
Natural numbers
Complex numbers
2.
If A = {1, 2, 5, 7} and B = {2, 4, 6}, how many subsets has A U B?
127
64
63
31
3.
If A = {1, 2, 3, 4, 5, 7, 8, 9} and B = {2, 4, 6, 7, 9} then find the number of proper subsets of A ∩ B?
16
15
32
31
4.
If U = {1,2,3,4,5} and A = {2,4} then A' should be
{2,4,5}
{2,4}
{1,2,3,4,5}
{1,3,5}
5.
In a survey of 1,000 consumers it is found that 720 consumers liked product A and 450 liked product B. What is the least number that must have liked both the products?
70
170
270
370
6.
Consider the following statements:
I. A = {1, 3, 5} and B = {2, 4, 7} are equivalent sets.
II. A = {1, 5, 9} and B = {1, 5, 5, 9, 9} are equal sets.
Which of the above statements is/are correct?
I only
II only
Both I and II
Neither I nor II
7.
A printing company charges ₵2.0645 for each wedding invitation it prints. What would be the cost before tax for printing 400 wedding invitations?.
₵825.80
₵8258.00
₵7858.00
₵785.80
8.
Given that (23 x 82) x 79 = 148994, find the exact value of (2.3 x 82) x 7.9.
14.8994
148.994
1489.94
14899.4
9.
If (3.14 x 18) x 17.5 = 3.14 x (3a x 17.5). Find the value of a.
3.0
5.8
6.0
9.0
10.
If 26039 oranges are shared equally among 13 boys, how many oranges does each boy receive?
23
203
230
2003
11.
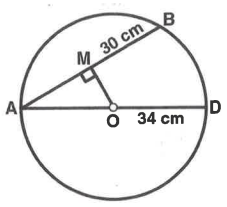
In the diagram, AD is the diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is
4 cm
8 cm
15 cm
17 cm
12.
Atwei bought meat weighing of a kilo. She put them evenly in three containers. How many kilos did she put in each container?
13.
A bakery uses bag of flour for each batch of cookies they make. The bakery used bag of flour yesterday. How many batches of cookies did the bakery make?
8 batches
9 batches
6 batches
10 batches
14.
Arrange the following in descending order of magnitude: 0.32,,27%,.
0.32,,27%,
0.32,,,27%
27%,0.32,,
,,0.32,27%
15.
The ratio 8:12 is equivalent to y:9. What is the value of y?
4
5
6
7
16.
Express 0.125 as a fraction in its lowest form.
17.
Out of 100 Oranges, 20% were eaten and 20% of the remaining were spoiled. Find the number of Oranges left?
16
32
64
128
18.
Find 25% of 75 kg.
1.875 kg
8.75 kg
18.75 kg
87.5 kg
19.
The population of a town increased from 2,000,000 to 2,800,000 in a decade. What is the increase in percentage?
25%
30%
35%
40%
20.
Simplify 7 x ( ÷ ) - .
21.
Divide 64.5 by 0.015, leaving the answer in standard form.
4.3 x 104
4.3 x 103
4.3 x 102
4.3 x 10
22.
The distance from the centre of a circle to any point on it is called?
circumference.
diameter.
radius.
sector.
23.
List the members of the set Q = {Prime factors of 30}.
{2, 3, 5}
{2, 6, 10}
{3, 5, 15}
{3, 6, 15}
24.
What is the place value of 7 in 24.376?
Unit
Ten
Tenth
Hundredth
25.
Abena spent of her money on sweets, on provisions and the rest on gari. What fraction of her money did she spend on gari?
26.
A man invested GH₵800.00 in a bank at a simple interest rate of 5% per annum. Find his total amount in the bank at the end of 1 years.
GH₵860.00
GH₵880.00
GH₵980.00
GH₵960.00
27.
The circumference of a circle is 440 m. Find the area of the circle.
[Take π = ]
14,400 m2
15,400 m2
16,400 m2
18,000 m2
28.
For what value of x is 10x = 1000?
1
2
3
4
29.
Evaluate 53-(-7)+(-15).
31
45
61
75
30.
Convert 2114five to a base ten numeral.
194
280
284
300
31.
The perimeter of a rectangle is 48 cm. If the length is 14 cm, find its width.
24 cm
20 cm
10 cm
3.4 cm
32.
If r = and s = , calculate 2r - 3s.
33.
There are 10 red and 15 green balls in a bag. Find the probability of selecting at random a red ball from the bag.
34.
Make n the subject of the relation θ = 180 - .
35.
If R = + , find R when d = 8 and h = 6.
3
4
4
4
36.
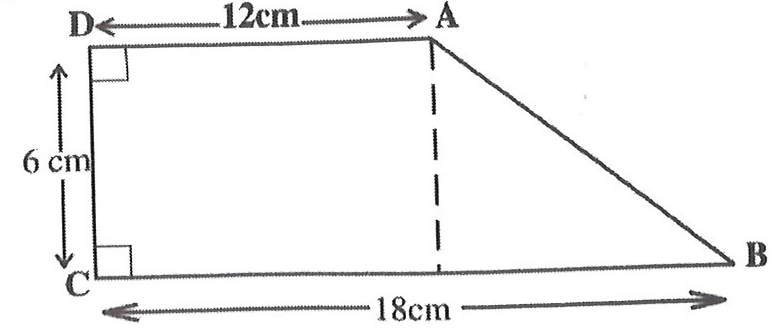
Calculate the area of the figure ABCD above.
72 cm2
90 cm2
108 cm2
126 cm2
37.
Find the H.C.F of 18, 36 and 60.
22 x 32 x 5
22 x 32
2 x 3 x 5
2 x 3
38.
Find the L.C.M of 10, 12 and 25.
90
120
150
300
39.
Correct 0.003858 to three significant figures.
0.00385
0.00386
0.0039
386
40.
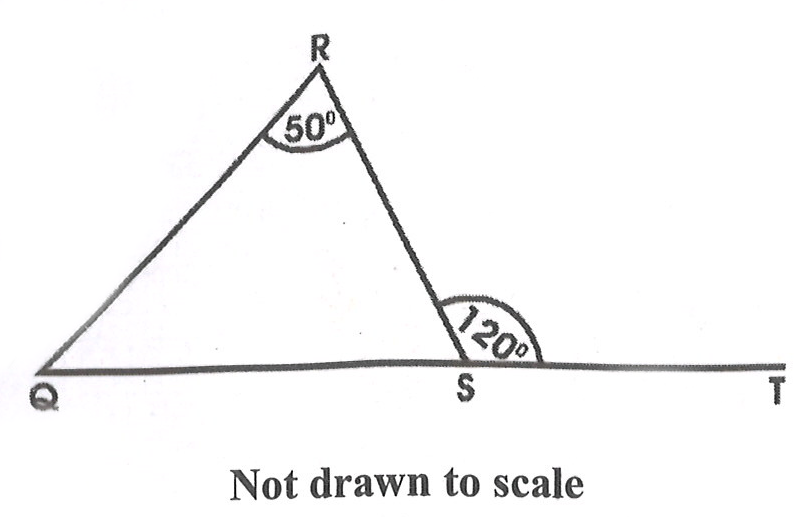
In the diagram, QRS is a triangle. Angle QRS = 50o and angle RST = 120o. Find angle RQS.
60o
65o
70o
80o
[1 hour]
Answer four questions only.
All questions carry equal marks.
All working must be clearly shown. Marks will not be awarded for correct answers without corresponding working..
(a)
In a class of 28 students, 14 passed Mathematics, 14 passed English and 6 passed neither Mathematics nor English.
(i)
Illustrate this information on a Venn diagram.
(ii)
How many students passed in both subjects.
(iii)
Find the probability of meeting a student who
(α)
passed in one subject only
(β)
passed in both subjects
(γ)
did not pass in any of the subjects
Let n represent the number of students who passed in both subjects.
(b)
A cylinder closed at both end has radius 7 cm and height 20 cm.
(i)
Find its total surface area.
(ii)
If the container is filled with milk to a depth of 5 cm before closing both ends, calculate:
(α)
The volume of milk in it.
(β)
The volume of the unfilled space.
[Take π = ]
(c)
Evaluate , leaving your answer in standard form.
(d)
26 ÷ (2 x 22) ÷ 25
(a)
Calculate
(b)
Three school children share some oranges as follows:
Akwesi gets of the total, and the remainder is shared between Abena and Jantuah in the ratio 3:2. If Jantuah gets 24 oranges, how many does Akwasi get?
(c)
Given that u = and v = , find (u + v).
(d)
m = 2p +
Make x the subject of this formula.
(a)
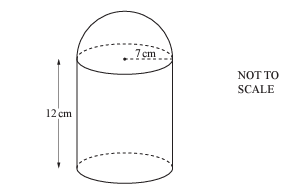
The diagram shows a solid made from a cylinder and a hemisphere, both of radius 7 cm. The cylinder has length 12 cm. Work out the total surface area of the solid.
[The surface area, A, of a sphere with radius r is 4πr2, π = . ]
(b)
The table below shows the distribution of pupils in a JHS form 1 who speak some of the Ghanaian languages.
| Ghanaian Language | No. of students who speak the language |
| Nzema | 5 |
| Ga | 20 |
| Twi | 30 |
| Ewe | 25 |
| Fante | 10 |
(i)
Draw a pie chart for the distribution
(ii)
What is the modal Ghanaian Language?
(ii)
If a pupil is selected at random from the form, what is the probability that he speaks Ga?
(iv)
If a pupil is selected at random from the form, what is the probability that he does not speak Ga?
(c)
Factorize completely 2ap + aq - bq - 2bp.
(a)
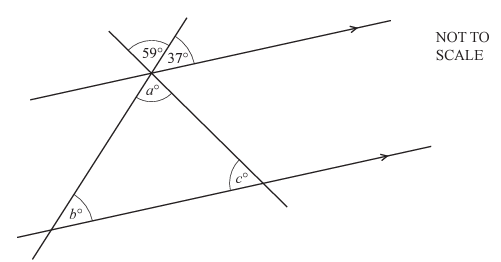
The diagram shows two parallel lines intersected by two straight lines. Find the values of a, b and c.
(b)
Given that f =
(i)
Make u the subject.
(ii)
Find u when f = 10 and v = 20.
(c)
(i)
Solve the inequality - ≥ 1
(ii)
Illustrate your answer on a number line.
(d)
Simplify of 6 ÷
(a)
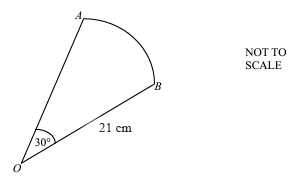
OAB is a sector of a circle with radius 21 cm and centre O. The angle at O is 30°.
(i)
Calculate the length of the minor arc AB
(ii)
Calculate the area of this sector
[Take π = ]
(b)
The table below shows the marks scored out of 10 by some candidates in a test.
| Mark | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of candidates | 2 | 3 | 5 | 7 | 8 | 13 | 7 | 5 |
(i)
From the table, find
(α)
the modal mark
(β)
how many candidates took the test.
(γ)
the mean mark for the test
(ii)
If 20% of the candidates failed,
(α)
how many failed?
(β)
What is the least mark a candidate should score in order to pass?
(γ)
What is the probability of selecting a student who passed the test?
(c)
Express 131five as a binary numeral.
(a)
(i)
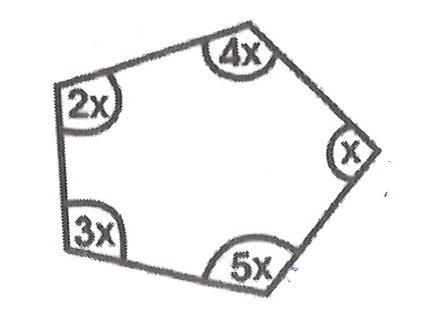
Find the value of x in the polygon above.
(ii)
A and B are subsets of a universal set
U = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18}
such that A = {even numbers} and B = {multiples of 3}.
(α)
List the elements of the sets A, B, (A∩B), (A∪B) and (A∪B)'.
(β)
Illustrate the information in (ii)(α) on a Venn diagram.
(b)
The following shows the distribution of marks of students in an examination.
| 6 | 43 | 26 | 18 | 27 |
| 42 | 8 | 22 | 31 | 39 |
| 55 | 44 | 37 | 47 | 59 |
| 10 | 12 | 36 | 53 | 48 |
(i)
Make a stem-and-leaf plot of the marks above.
(ii)
Find the probability of selecting a student who scored between 40 and 50.
(iii)
Find the number of students who passed the examination, if the pass mark was 30.
(c)
Use the following points to answer the questions below
A(0,3), B(2,3) and C(4,5)
(i)
Find the image A1B1C1 of ABC under a translation by the vector
(ii)
Using the x-axis as the mirror line, find the image A2B2C2 of ABC.
(iii)
Using the y-axis as the mirror line, find the image A3B3C3 of ABC.
(iv)
Find the enlargement A4B4C4 of ABC with scale factor -1.
(v)
Find the image A5B5C5 of ABC under the anticlockwise rotation through 90o about the origin.
(vi)
Find the image A6B6C6 of ABC under the clockwise rotation through 90o about the origin.
(vii)
Find the image A7B7C7 of ABC under the anticlockwise rotation through 180o about the origin.
(viii)
Find the image A8B8C8 of ABC under the clockwise rotation through 180o about the origin.
(ix)
Find A1B1⃗
(x)
Find the gradient between the points A(0,3) and C(4,5)