1.
Express 0.0098 in the standard form.
9.8 x 10-3
9.8 x 10-2
9.8 x 102
9.8 x 103
2.
If 2m - 2 = 32, find the value of m.
4
5
6
7
3.
Find the gradient of the line joining the points P(-2, 6) and Q(3, -2).
-
-
4.
The marks obtained by 10 candidates in a test are: 8, 6, 2, 2, 4, 8, 9, 4, 9, 3. What is the median mark?
6
5.5
5
4.5
5.
The mean age of a group of 5 boys is 4. If the mean age of 4 of them is 4, what is the age of the remaining boy?
5
4
3
6
6.
A water tank is a cube of side 2 m. The depth of water in it is 60 cm. What is the volume of water in the tank?
2.4 m3
4 m3
8 m3
24 m3
7.
If a = and b = , find 3a - b
8.
P(-2, 1) and Q(-1, 2) are two points. Find PQ→.
9.
Find the vector which translates the point (1, 3) to the point (3, -2).
10.
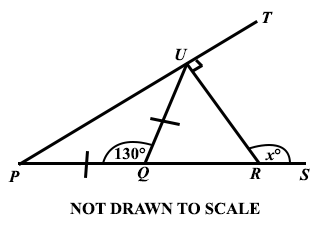
In the diagram PQRS and PUT are straight lines. ∠PQU = 130°.
Find x.
140°
120°
115°
110°
11.
Find the rule for the mapping:
| x | 1 | 2 | 3 | 4 | 5 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| y | 4 | 2 | 0 | -2 | -4 |
y = 2x + 2
y = -2x + 2
y = 4x
y = -2x + 6
12.
Find the value of a3 + 2ab2 + b3, when a = 2 and b = -1.
9
11
12
13
13.
In a class of 40 students, 30 of them read Chemistry and 20 read Physics. What is the probability that a student chosen at random in the class read both Chemistry and Physics?
14.
Make h the subject of the relation V = πr2h
15.
PQ→ = , RQ→ = . Find PR→.
16.
Three people shared an amount of GH₵ 300.00 in the ratio 1 : 2 : 3. Find the highest amount received.
GH₵ 50.00
GH₵ 100.00
GH₵ 150.00
GH₵ 200.00
17.
The bearing of a point Q from another point P is 040°. Find the bearing of P from Q.
220°
160°
130°
040°
18.
If P = {3, 4, 5, 6}, Q = {5, 6, 7, 8} and R = {2, 3, 7, 9}.
Which of the following represents the set P ∩ (Q ∪ R)?
{5, 6}
{3, 4, 5}
{3, 5, 6}
{3, 4, 5, 6}
19.
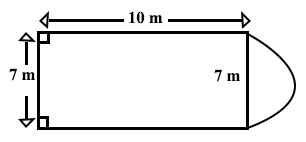
The diagram above represents a compound which is made up of a rectangle portion, 7 m by 10 m and a semi-circle portion.
Calculate the perimeter of the compound.
[Take π = ]
38 m
45 m
49 m
56 m
20.
Simplify 3 - 2
30
20
15
10
21.
Find the length of vector
125
15
5
22.
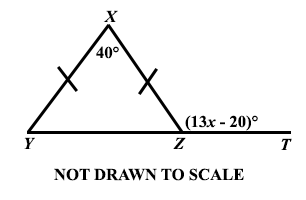
In the triangle XYZ is produced to T, ∠YXZ = 40° and ∠XZT = (13x - 20)°.
Find the value of x.
10
20
110
130
23.
Solve - = 1
-6
-1
1
6
24.
If 6x : 64 = 18 : 32, find the value of x
1
2
3
6
25.
Evaluate 1 - (1 ÷ 2)
2
1
26.
Solve the inequality 48 < (1 + x)
x > 97
x > 96
x > 95
x < 95
27.
A box contains 40 pens of equal size. 10 of them are green and 18 red. If a pen is chosen at random from the box, what is the probability that it is neither green nor red?
28.
The height of an isosceles triangle is 4 cm. Find the length of the base, if the other sides are 5 cm long.
3 cm
4 cm
5 cm
6 cm
29.
Evaluage
4
8
16
32
30.
If 2(kx + 6) = 6 + 8x, find the value of k when x = 3.
4
3
-3
-4
31.
Solve the equation - 2 =
-7
-4
1
7
32.
Given that 25x = 1, find x.
0
1
2
33.
A bag contains 12 good oranges and 9 bad oranges. If an orange is picked at random from the bag, what is the probability that it is a good orange?
34.
The sum of two numbers is 72. The difference between them is 26. Find the smaller number.
23
28
36
49
35.
The ratio of sheep to goats on a farm is 2 : 3. If there are 150 goats, how many sheep are there on the farm?
50
100
200
60
36.
M = {1, 2, 3, 8, 10} and N = {8, 1, x, 3, 2}.
If M is equal to N, what is the value of x?
1
2
3
10
37.
In the Venn diagram Q is the set of numbers inside the circle and R is the set of numbers inside the triangle.
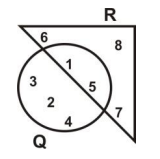
Find Q ∩ R.
{1, 5}
{2, 3, 4}
{6, 7, 8}
{1,2,3,4,5}
38.
If (23 × 82) × 79 = 148,994, find the exact value of (2.3 × 82) × 7.9
1.48994
14.8994
148.994
1489.94
39.
Which of the following inequalities is represented by the number line?
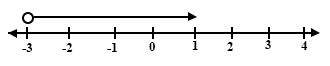
x ≤ -3
x ≥ -3
x > -3
x < -3
40.
It takes 15 men, 48 days to weed a plot of land. How many men can weed the same plot of land in 16 days, if they work at the same rate?
5
45
18
32
(a)
Evaluate + , when x = 2, y = -3 and z = 4.
(b)
Find Q if 3Q + 132 = 162.
(c)
In a class of 50 students, 30 offer Economics, 17 offer Government and 7 offer neither Economics nor Government.
(i)
Illustrate the information on a Venn diagram.
(ii)
Find:
(α)
how many students offer both subjects
(β)
the probability that a student selected at random from the class offers only one subject
(a)
Evaluate
(b)
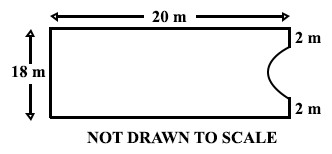
The diagram above represents a rectangular compound 20 m by 18 m with a semi-circular portion cut off.
Calculate
(i)
the perimeter of the compound
(ii)
the area of the compound.
[Take π = ]
(a)
Find the truth set of the inequality
- ≤ 1
Illustrate your answer on the number line.
(b)
Simplify: , leaving the answer in standard form.
(c)
A train fare for a school child is half the fare of a teacher. The total fare for 120 children and 15 teachers for an excursion is GH₵ 300.00.
(i)
Find the fare of a child.
(ii)
How many children will go on the excursion with 20 teachers for a total fare of GH₵ 400.00.
The table below gives the frequency distribution of the marks obtained in a class test by a group of 64 pupils.
| Marks (Out of ten) | Frequency |
| 2 | 9 |
| 3 | 14 |
| 4 | 13 |
| 5 | 10 |
| 6 | 5 |
| 7 | 8 |
| 8 | 2 |
| 9 | 3 |
(a)
Draw a bar chart for the distribution.
(b)
A pupil is chosen at random from the class. What is the probability that the pupil obtained 7 marks?
(a)
Make u the subject of the relation = .
(b)
A rectangular tank of sides 4 m by 8 m by 11 m has the same volume as a cylindrical tank of height 7 m.
Calculate the base radius of the cylindrical tank.
[Take π = ]
(c)
Badu is four times as old as Juliet. In 10 years Badu will be twice as old as Juliet. Find Juliet's age.
Using a scale of 2 cm to 2 units on each axis, draw on a sheet of graph paper two perpendicular axes 0X and 0Y, for intervals -10 ≤ x ≤ 10 and -10 ≤ y ≤ 10.
(a)
Draw ∆ABC with coordinates A(6, 8), B(2, 5) and C(7, 2).
(b)
Draw the image ∆A1B1C1 of ∆ABC under an enlargement with scale factor -1 from the origin where A → A1, B → B1 and C → C1. Label vertices and coordinates clearly.
(c)
Draw the image ∆A2B2C2 of ∆ABC under a clockwise rotation of 270° about the origin where A → A2, B → B2 and C → C2. Label vertices and coordinates clearly.
(d)
(i)
What transformation maps ∆A1B1C1 onto ∆A2B2C2?
(ii)
What is the equation of BB1?