2⁶ ÷ (2² x 2¹) ÷ 2⁵.

Concepts

BODMAS

BODMAS is an acronym to help students remember the order of mathematical operations – the correct order in which to solve maths problems.

Bodmas stands for B-Brackets, O-Orders (powers/indices or roots), D-Division, M-Multiplication, A-Addition, S-Subtraction

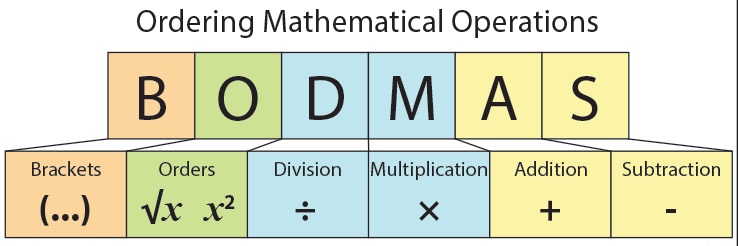
Therefore in the above equation, we will simplify the one in the bracket first

Law of indices

Indices

An index is a small number that tells us how many times a term has been multiplied by itself.

The plural of index is indices.

Indices are expressed in the form a^m

Where a is the base and m is the power

The law of indices only apply to indices which has the same base

The Multiplication Law

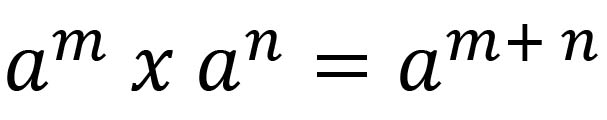
States that if the bases are the same and they are multiplying, you simply add the powers

The Division Law

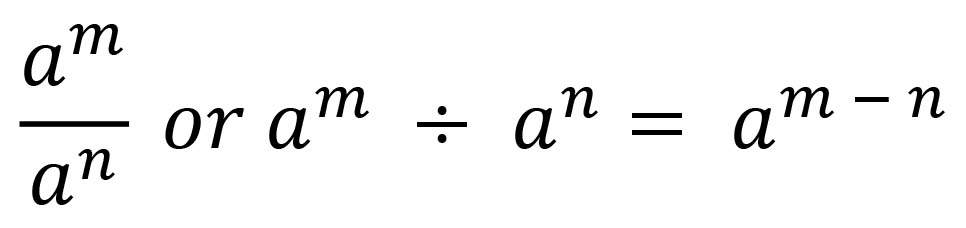
States that if the bases are the same and they are dividing, you simply subtract the power of the denominator base from the power of the numerator base

The Negative Power Law

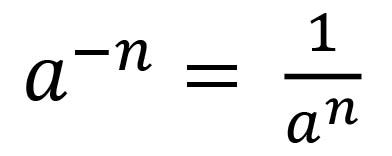
States that if the power is negative its the same as 1 over the positive power of the base

Solving the one in the bracket

2² x 2¹

From the multiplication law of indices

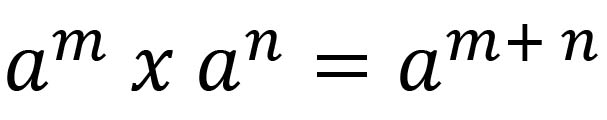
2² x 2¹ = 2²⁺¹ = 2³

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2⁶ ÷ (2³) ÷ 2⁵

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2⁶ ÷ 2³ ÷ 2⁵

Solving 2⁶ ÷ 2³

From the division law of indices

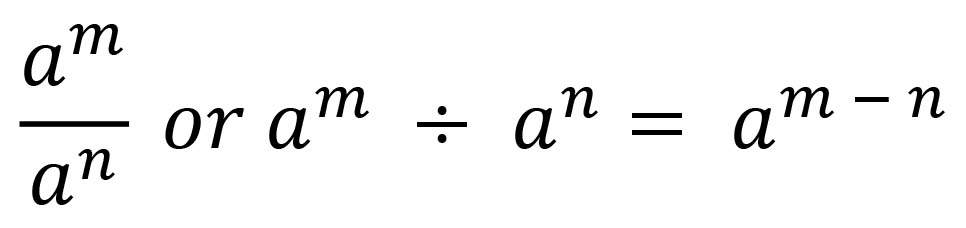
2⁶ ÷ 2³ = 2^6-3 = 2³

2⁶ ÷ 2³ ÷ 2⁵ = 2³ ÷ 2⁵

Solving 2³ ÷ 2⁵

From the division law of indices

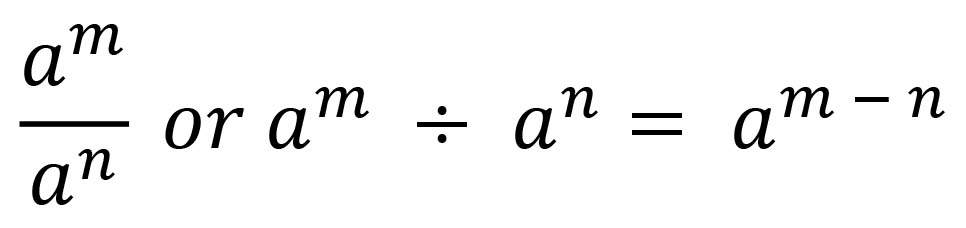
2³ ÷ 2⁵ = 2^3-5 = 2^-2

Applying the negative power law to simplify further

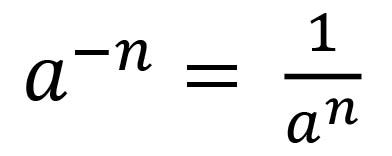
2^-2 = 1/2² = 1/4 = 0.25

In Summary

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2⁶ ÷ (2²⁺¹) ÷ 2⁵

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2⁶ ÷ (2³) ÷ 2⁵

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2⁶ ÷ 2³ ÷ 2⁵

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2^6-3 ÷ 2⁵

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2³ ÷ 2⁵

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2^3-5

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 2^-2

2⁶ ÷ (2² x 2¹) ÷ 2⁵ = 1/2² = 1/4 = 0.25