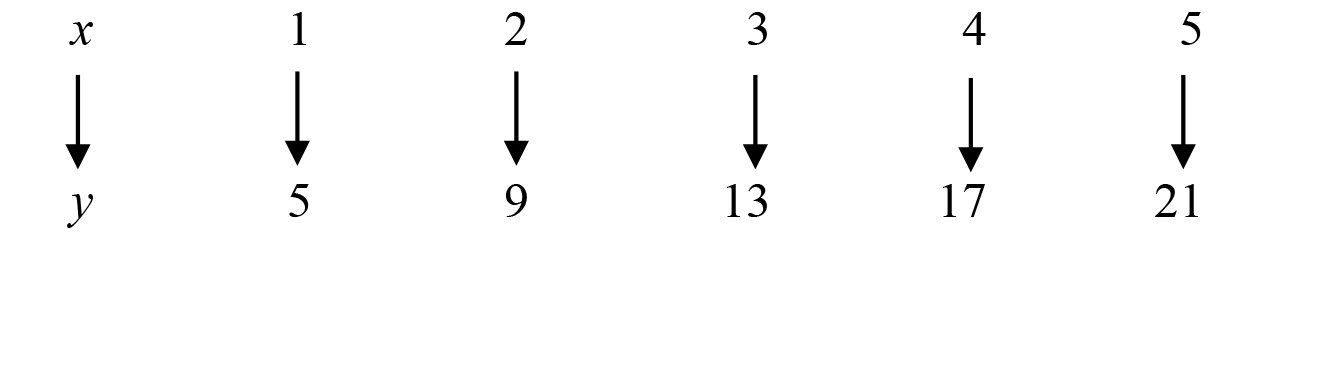
Find x when y = 37 for the above mapping
Find the rule of the mapping first
Check if the mapping is a linear/arithmetic sequence by finding the difference between each consecutive value of y. A linear sequence has the common difference between consecutive numbers the same
If it is linear, use the equation of linear formula to find the rule of the mapping
y2 - y1 = 9 - 5 = 4
y3 - y2 = 13 - 9 = 4
y4 - y3 = 17- 13 = 4
y5 - y4 = 21 - 17 = 4
As you can see, the rule of the mapping is a linear since the difference is the same, hence use the linear sequence formula to find the rule
Un = U1 + (n-1)d
Where Un is the value at the nth position, in the rule of mapping, the y value
U1 is the first term, in the mapping above, 5
d is the common difference between each consecutive terms
n is the position, in the case of the above mapping, x
y = 5 + (x-1)4
y = 5 + (x-1) x 4
y = 5 + x x 4 -1x4
y = 5 + 4x-4
y = 4x+5-4
y = 4x+1
We can test with when x = 3
y = 4x+1
y = 4 x 3+1
y = 12+1 = 13
You can try the values of x to see if you will get the corresponding y value to prove the rule is correct
| x |
y = 4x+1 |
y |
| 1 |
y = 4x1+1 = 4+1 = 5 |
5 |
| 2 |
y = 4x2+1 = 8+1 = 9 |
9 |
| 3 |
y = 4x3+1 = 12+1 = 13 |
13 |
| 4 |
y = 4x4+1 = 16+1 = 17 |
17 |
| 5 |
y = 4x5+1 = 20+1 = 21 |
21 |
y = 4x+1
y = 37
37 = 4x+1
Make x the subject
37 - 1 = 4x
36 = 4x
Divide both sides by 4
36/4 = 4x/4
9 = x

