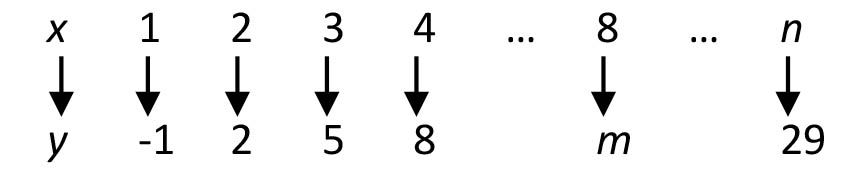
Check if the mapping is linear sequence. For a liner/arithmetic mapping or sequence, the common difference (substraction of consecutive values of y are the same
For a liner sequence u1, u2, u3, u4, u5,...,un
Common Difference = u2 - u1 = u3 - u2 = u4 - u3 = u5 - u4, ... = un - un-1
Values of y are -1, 2, 5, 8, ...,m,...29
Common Difference = 2--1 = 5-2 = 8-5 = 3
You can see that all the calculations of the common differences are the same (3), hence the mapping is linear
For a linear mapping, the rule of the mapping is calculated by the formula below:
y = y1 + (x-1)d
Where y1 = the first term (value) of y and d = the common difference
From the above mapping, the first term of y is -1 and the common difference is 3
Hence the rule of the mapping is calculated as below:
y = -1 + (x-1)3
Expand the bracket and simplify the expressions
y = -1 + xx 3 -1x3
y = -1 + 3x -3
y = 3x -1-3
y = 3x -4