First determine the type of the sequence

A sequence is an enumerated collection of objects in which repetitions are allowed and order matters.

Types of Sequences

1. Linear/Arithmetic sequences

Sequences where the difference between each term is the same. Terms add (or subtract) the same number each time.

Example

The number added or subtracted is called common difference. To find the common difference, substrate the (n-1)^th term from the nth term. The common difference is supposed to be the same for all substations if it’s a linear sequence. If it’s not the same, then the sequence is not a linear sequence.

To find the n^th term of a linear/arithmetic sequence, the formula below is used:

a_n = a₁ + (n-1)d
where a₁ = first term
n = the position you are finding
d = the common difference (a_n –a_(n-1))

For example to find the 5^th term for the sequence, 3,5,7,9,...,... we can apply the above formula.

n = 5
a₅ = a₁+(5-1)d
d = 5 -3 = 7 – 5 = 9 – 7 = 2
a₁ = first term = 3

Hence the 5^th term = 3 +(5-1) x 2 = 3 + 4 x 2 = 11

Let's determine if the given sequence is linear or not.

2, 5, 10, 17,....., ......

Common Difference = 5 – 2 = 3 or 10 -5 = 5 or 17 – 10 = 7, since the common differences are not the same, the sequence can’t be a linear sequence.

2. Geometric progressions

Geometric sequences / progressions are similar to linear sequences, but instead of adding/subtracting the same number each time, you multiply (or divide) by the same number each time.

Example

The term multiplied or divided is called common ratio. The common ratio is calculated by dividing the nth term by the (n-1)th term.

Thus for the above example 2, 4, 8, 16, the common ratio can be calculated as
4/2 = 8/4 = 16/8 = 2

The common ratio for each consecutive terms must be the same. If not, then the sequence is not geometric.

Let’s determine if the sequence in the question is geometric

2, 5, 10, 17, ....., ......

Common ratio = 5/2 or 10/5 or 17/10

As you can see the common ratios are not the same so the sequence can’t a geometric sequence.

3. Fibonacci sequences

Fibonacci sequences are sequences where each term is the sum of the previous two terms. In a Fibonacci sequence, the first two numbers must be chosen before starting the sequence. The most common sequence begins with 0 and 1. This specific sequence of numbers generated by 0 and 1 are known as the "Fibonacci numbers".

Examples

Let's determine if the sequence in the question is a Fibonacci sequence

2, 5, 10, 17, ....., ......

The 3^rd term is supposed to be 2 + 5 = 7 but its 10, hence the sequence is not a Fibonacci sequence.

4. Quadratic sequences

Quadratics are expressions in which the highest power of x is an x² term. The general term of a quadratic sequence is ax² + bx + c. For example, 2x² + 3x + 2 is a quadratic because the highest power of x is x². However, x³ – 2x² is not a quadratic, because although it contains an x² term, there is a higher power of x (the x³).

In quadratic sequences, the differences between the terms are not the same, however the difference of the differences are the same. This is the only way you can identify them.

Take the examples below. You will see that the differences between the terms (in red) are different.

However the differences of the red terms (in green) are the same.

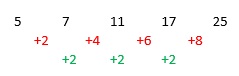
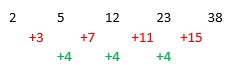
Let's check if the sequence in the question is quadratic or not.

2, 5, 10, 17, ....., ......

2      5      10      17   

   +3   +5    +7

      +2     +2

As you can see, the sequence is a quadratic sequence. Hence we have to find the quadratic equation that generates the sequence.

Finding the formula for a quadratic sequence

The general formula for a quadratic sequence is U_n = an² + bn + c

The a, b and c can be obtained by the formula below:
2a = the second difference
3a + b = U₂ – U₁
a + b + c = U₁

Where U₂ – U₁ is the difference between the first and the second terms of the sequence.
U₁ is the first term

We can now apply the above formula to find the equation for the sequence

2, 5, 10, 17, ....., ......

2      5      10      17   

   +3   +5    +7

      +2     +2

The second difference (the one in green color) is 2.

Hence 2a = 2, solving for a, a = 2/2 = 1 ---------- equation (1)

3a + b = U₂ – U₁

U₁ (the first term) = 2

U₂ (the second term) = 5, hence the difference (U₂ – U₁) = 5 – 2 = 3

Hence 3a + b = 3, substitute a = 1 from equation 1 in this equation.

3(1) + b = 3, b = 3-3 = 0, hence b = 0

Since we know a and b, we can find c

a + b + c = U₁

U₁ (the first term) = 2

Hence 1 + 0 + c = 2, c = 2-1 = 1, hence c = 1

U_n = an² + bn + c

Hence U_n = (1)n² + (0)n + 1

1 x n² = n² , 0 x n = 0, hence

U_n = n² + 1

Now we can find the 5^th and 6^th terms

U₅ = 5² + 1 = 25 + 1 = 26

U₆ = 6² + 1 = 36 + 1 = 37

Hence the 5^th and 6^th terms are 26 and 37 respectively.

You can verify the already given terms with the obtained formula to prove the formula is correct

n (Term)	n2 + 1	Result
1	12 + 1 = 1 + 1	2
2	22 + 1 = 4 + 1	5
3	32 + 1 = 9 + 1	10
4	42 + 1 = 16 + 1	17