1.
Simplify:
2.
-
-1
-2
3.
In a class of 39 student, 25 offer Fante and 19 offer Twi. Five student do not offer any of the two languages. How many student offer only Twi?
4.
Evaluate
- 1
2 - 1
+ 1
2 + 1
5.
Mary and charity entered into a business partnership and agreed to share their profit in the ratio 4 : 5 respectively. If Mary received GH₵ 5,000.00 less than Charity, how much profit did they make?
GH₵ 30,000.00
GH₵ 35,000.00
GH₵ 40,000.00
GH₵ 45,000.00
6.
A man bought a car which costs ₦5,000,000.00 from a dealer on hire purchase. He pays a deposit of ₦3,000,000.00 and agrees to pay the balance at 8% compound interest per annum. If he pays ₦1,000,000.00 at the end of each year, how much will be remaining to be paid after two years?
7.
y varies inversely as the square of x. When x = 3, y = 100.
Find the value of x when y = 25.
x = 30
x = 12
x = 6
x = 5
8.
Solve the equation: t - = -1
t =
t =
t =
t =
9.
Find the truth set of the equation (x - 2)2 + 3 = (x + 1)2 - 6.
{-2}
{-1}
{1}
{2}
10.
Two friends, Dede and Kofi decided, to buy the same type of car. They found out that the car cost ₦3,000,000.00. The amount of money (f) which Dede had was not enough to buy the car but Kofi had enough money (k) to buy the car. Which of the of the following inequalities is true?
f ≤ ₦3,000,000.00 ≤ k
f > ₦3,000,000.00 > k
f < ₦3,000,000.00 ≤ k
f ≥ ₦3,000,000.00 ≥ k
11.
Simplify: -
12.
Simplify:
xy
13.
A chord of a circle with radius 5 cm subtends an angle of 70° at the centre.
Find, correct to one decimal place, the length of the chord.
8.2 cm
5.7 cm
4.1 cm
2.9 cm
14.
A pyramid with a square base has a volume of 1,400 cm3. If a side of the base is 10 cm long, find the height of the pyramid.
70 cm
42 cm
21 cm
7 cm
15.
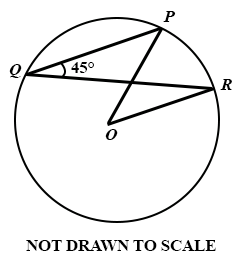
In the diagram, O is the centre of the circle. If the radius of the circle is 12 cm and ∠ PQR = 45°, calculate, correct to the nearest cm, the length of arc PR.
[Take π = ]
113 cm
57 cm
19 cm
15 cm
16.
Which of the following about parallelograms is true?
Opposite angles are supplementary
Opposite angles are complementary
Opposite angles are equal
Opposite angles are reflex angles
17.
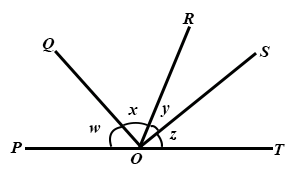
In the diagram, POT is a straight line. If (w + x + y) = 140° and (x + y + z) = 130°, find the value of (x + y).
40°
50°
90°
110°
18.
The interior angles of a pentagon are x°, (x + 5)°, (x + 10)°, (x + 15)° and (x + 20)°.
Find the value of x.
98
88
78
68
19.
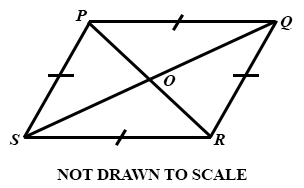
The diagram shows a rhombus PQRS with diagonals intersecting at O.
If the ratio of ∠ PQR to ∠ QPS is 3 : 7, calculate the value of ∠ QSR.
27°
45°
54°
63°
20.
Calculate the gradient of the line which passes through the points (1, 4) and (-2, 6).
-
-
21.
Calculate the distance between points (3, -2) and (8, 10).
12 units
13 units
14 units
15 units
22.
Evaluate +
3
2
1
0
23.
From a height of 2 m above the ground and at a horizontal distance of 12 m from a tree, the angle of elevation of the top of the tree is 30°.
How tall is the tree?
8 m
8 m
14 m
18 m
24.
Express the bearing of 312° in compass direction form.
S 48° W
N 48° W
S 48° E
N 48° E
25.
A fair die is thrown once. What is the probability of obtaining 3?
1
26.
The table shows the distribution of the ages of members of a school choir.
Use the table to answer the question below
| Age(years) | 15 | 16 | 17 | 18 |
| No. of students | 5 | 6 | 3 | 1 |
Calculate the mean age.
15 years
16 years
17 years
18 years
27.
The table shows the distribution of the ages of members of a school choir.
Use the table to answer the question below
| Age(years) | 15 | 16 | 17 | 18 |
| No. of students | 5 | 6 | 3 | 1 |
Find the median age.
15 years
16 years
16 years
17 years
28.
If x = and m = , express x in terms of v, y and n.
x =
x =
x =
x =
29.
If Msix = 123five, find the value of M.
53
55
62
102
30.
In triangle XYZ, |XY| = 8 cm and Z is equidistant from X and Y.
If Z is 5 cm from X, find the area of the triangle.
24 cm2
18 cm2
12 cm2
10 cm2
31.
Calculate the total surface area of a cuboid whose dimensions are 12 cm x 8 cm x 3 cm.
96 cm2
156 cm2
288 cm2
312 cm2
32.
Calculate, correct to the nearest whole number, the volume of a sphere with diameter 6 cm.
[Take π = ]
15 cm3
36 cm3
113 cm3
124 cm3
33.
The diagram shows a circle centre O. Use it to answer the question below.
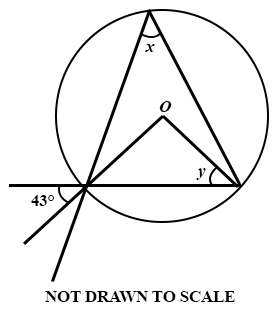
Find the value of y.
43°
47°
54°
86°
34.
The diagram shows a circle centre O. Use it to answer the question below.

Find the value of x.
43°
47°
54°
86°
35.
Find the nth term of the Geometric Progression (G.P): , , , ...
2n - 1
2n
36.
An old man goes for a walk every 6 days. If he went for a walk on Wednesday, when will he go for the next walk?
Monday
Tuesday
Wednesday
Thursday
37.
The cumulative frequency curve (Ogive) shows the distribution of waiting time of some customers at a filling station. Use the curve to answer the question below.

Estimate the interquartile range.
0.70
0.75
0.80
0.85
38.
The cumulative frequency curve (Ogive) shows the distribution of waiting time of some customers at a filling station. Use the curve to answer the question below.

How many customers waited for at least 3 minutes?
16
17
18
19
39.
What is the coefficient of x in the expansion of (4x2 + 3x - 1)(3x + 1)?
-1
0
1
2
40.
Find the quadratic equation whose roots are and -.
x2 + 4x - 3 = 0
4x2 + x - 3 = 0
x2 - 4x - 3 = 0
4x2 + 4x - 3 = 0
41.
Two times a number added to one-third of the number gives 5. Find the number.
2
2
2
2
42.
Find the mean deviation of 5, 8, 3, 7, 2.
0
2
5
10
43.
In a certain community, 1 out of every 8 persons is a graduate. If Yoni and Etteh are members of the community, what is the probability that they are both graduates?
44.
Which of the following statements is false?
In a circle, equal chords subtend equal angles at the centre
The length of an arc is proportional to the angle subtended by the arc at the centre of the circle
The circumference of a circle is directly proportional to its diameter
The angle between the tangent to a circle and its radius is complementary
45.
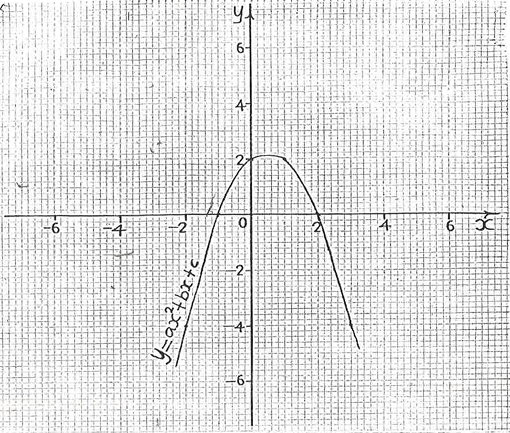
Find the equation of the graph in the diagram.
y = 2 - x - x2
y = 2 - x + x2
y = 2 + x - x2
y = 2 + x + x2
46.
If log x = 0.3030, log y = 0.4777 and log Z = 0.8451; evaluate:
1.4313
0.8466
0.5466
0.0149
47.
Consider these two statements:
P:n is an odd number;
Q:n is a prime number greater than 2.
Express "If n is not an odd number then n is not a prime number greater than 2" in symbolic form.
~P ∧ ~Q
~P ⇒ Q
P ⇒ ~Q
~P ⇒ ~Q
48.
Which of the following is not a rational number?
-5
3
49.
Use the diagram to answer the question below
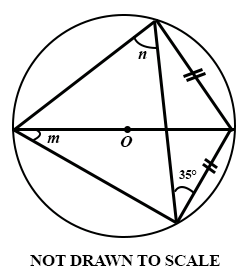
Find the value of m.
35°
45°
65°
75°
50.
Use the diagram to answer the question below

Find the value of n.
70°
65°
55°
35°
(a)
Solve, correct to one decimal place, tan(θ + 25°) = 5.145, where ° ≤ θ ≤ 90°.
(b)
In the relation t = m:
(i)
make n the subject of the relation;
(ii)
find the positive value of n when t = 25, m = 5 and r = 4.
The first three terms of an Arithmetic Progression (A.P.) are (x + 1), (4x – 2) and (6x – 3) respectively.
If the last term is 18, find the:
(a)
value of x;
(b)
sum of the terms of the progression.
The angle of a sector of a circle with radius 22 cm is 60°. If the sector is folded such that the straight edges coincide, forming a cone, calculate, correct to one decimal place, the
(a)
radius;
(b)
height;
(c)
volume of the cone.
[Take π = ]
(a)
In how many years will GH₵ 312.50 invested at 4% per annum simple interest amount to GH₵ 500.00?
(b)
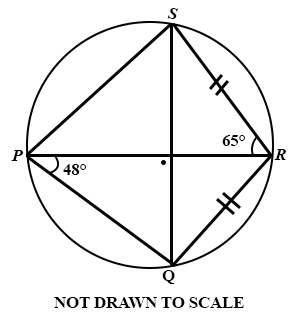
In the diagram, PQRS is a cyclic quadrilateral. If |SR| = |RQ|, ∠SRP = 65° and ∠RPQ = 48°, find ∠PRQ.
(a)
The probabilities that James and Juliet will pass an examination are and respectively. Find the probability that both will fail the examination.
(b)
| Balls | Green | Blue |
| New | 8 | 2 |
| Old | 4 | 6 |
The table shows the distribution of balls in a bag. If 2 balls are selected at random with replacement, find the probability of selecting either 2 new green balls or 2 old blue balls.
(a)
If 9x x 32y = , and 2-x x 4-y = , find the values of x and y.
(b)
Two commodities X and Y cost D70.00 and D80.00 per kg respectively. If 34.5 kg of X is mixed with 26 kg of Y and the mixture is sold at D85.00 per kg, calculate the percentage profit.
(a)
Copy and complete the following table for the relation: y = 2(x + 2)2 - 3 for -5 ≤ x ≤ 2.
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
| y | -1 | -3 | 5 |
(b)
Using scales of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of the relation y = 2(x + 2)2 - 3 for -5 ≤ x ≤ 2.
(c)
Use the graph to find the solution of:
(i)
2(x + 2)2 = 3;
(ii)
2(x + 2)2 = 5.
(d)
For what values of x, from the graph is y increasing in the interval?
(a)
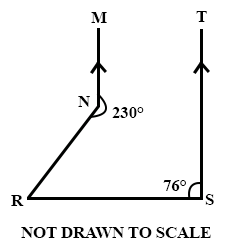
In the diagram, MN // ST, ∠MNR = 230° and ∠TSR = 76°.
Find the value of ∠NRS.
(b)
(i)
Copy and complete the tables for the addition ⊕ and multiplication ⊗ in modulo 5.
| ⊕ | 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 | 0 |
| 2 | 3 | |||
| 3 | 4 | 2 | ||
| 4 | 0 |
| ⊗ | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | |||
| 3 | 2 | |||
| 4 | 1 |
(ii)
Use the tables to find:
(α)
4 ⊗ 2 ⊕ 3 ⊗ 4;
(β)
m such that m ⊗ m = m ⊕ m;
(γ)
n such that 3 ⊕ n = 2 ⊗ n.
(a)
If 16n = , find the value of n.
(b)
The perimeter of a square and a rectangle is the same. The width of the rectangle is 6 cm and its area is 16 cm2 less than the area of the square. Find the area of the square.
The table shows the distribution of marks scored by 500 candidates in an examination.
| Marks | 0 - 9 | 10 - 19 | 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 | 60 - 69 | 70 - 79 | 80 - 89 | 90 - 99 |
| Frequency | 10 | 28 | 40 | 92 | y + 60 | 90 | 50 | 30 | 15 | 5 |
(a)
Find the value of y.
(b)
Construct a cumulative frequency table and use it to draw a cumulative frequency curve.
(c)
Use the curve to estimate the probability of selecting a candidate who scored not more than 45%.
The angle of elevation of the top, X, of a vertical pole from a point, W, on the same horizontal ground as the foot, Z, of the pole is 60°. If W is 15 km from X and 12 km from a point Y on the pole,
(a)
illustrate this information with a diagram.
(b)
calculate, correct to two decimal places, the:
(i)
angle of elevation of Y from W;
(ii)
length, XY.
(a)
Using scales of 2 cm to 2 units on both axes, draw on a sheet of graph paper two perpendicular axes 0x and 0y for -10 ≤ x ≤ 10 and -10 ≤ y ≤ 10.
(b)
Given point E(3, 2), F(-1, 5) and the vectors FG→ = and GH→ = , find the coordinates of the points G and H.
(c)
Draw, on the same graph, indicating clearly the vertices and their coordinates, the
(i)
quadrilateral EFGH;
(ii)
image E1F1G1H1 of the quadrilateral EFGH under an anticlockwise rotation of 90° about the origin where E → E1, F → F1, G → G1 and H → H1.
(d)
The side E1F1 of the quadrilateral E1F1G1H1 cuts the x-axis at the point P.
Calculate, correct to one decimal place, the area of E1H1G1P1.
(a)
Given that P = , Q = , R = and PQ = R, find the values of x, y and z
(b)
(i)
Draw on a graph paper, using a scale of 2 cm to 1 unit on both axes, the lines x = 1; y = 2; and x + y = 5.
(ii)
Shade the region which satisfies simultaneously the inequalities x + y ≤ 5; y ≥ 2 and x ≥ 1