1.
Express, correct to three significant figures, 0.003597.
0.00359
0.00360
0.004
0.359
2.
Evaluate .
-
-
3.
Solve: - = 4
y = 29
y = -29
y = -19
y = 19
4.
Simplify, correct to three significant figures, (27.63)2 - (12.37)2.
610
611
612
614
5.
If 7 + y = 4(mod 8), find the least value of y. 10 ≤ y ≤ 30.
21
19
13
11
6.
If T = {prime numbers} and M = {odd numbers} are subset of µ = {x : 0 < x ≤ 10, and x is an integer}, find ( T' ∩ M' )
{1,2,3,5,7,8,9}
{1,2,4,6,8,10}
{1,4,6,8,10}
{4,6,8,10}
7.
| log3 9 - log2 8 |
| log3 9 |
-
-
8.
If 23y = 1111two, find the value of y.
7
6
5
4
9.
If 6, p and 14 are consecutive terms in Arithmetic Progression (A.P), find the value of p.
8
6
10
9
10.
Evaluate : 2 - 3 +
4 +
4 - 9
4 - 11
4 - 21
11.
If m : n = 2 : 1, evaluate :
12.
H varies directly as p and inversely as the square of y. If H = 1, p = 8 and y = 2, find H in terms of p and y.
H =
H =
H =
H =
13.
Solve 4x2 - 16x + 15 = 0
x = -1 or -2
x = 1 or -1
x = 1 or 2
x = 1 or -2
14.
Evaluate , leaving the answer in standard form.
1.639 x 10-2
1.639 x 10-1
1.639 x 101
1.639 x 102
15.
Simplify: log106-3log103+log1027.
2log103
log103
log102
3log102
16.
Bala sold an article for ₦6,900.00 and made a profit of 15%. calculate his percentage profit if he had sold it for ₦6,600.00.
13%
12%
10%
5%
17.
If 3p = 4q and 9p = 8q - 12, find the value of pq
-12
-7
7
12
18.
If (0.25)y = 32, find the value of y.
-
-
19.
There are 8 boys and 4 girls in a lift. What is the probability that the first person who steps out of the lift will be a boy?
20.
Simplify:
21.
Which of these values would make undefined?
-1
-
1
22.
The total surface area of a solid cylinder is 165 cm2. If the base diameter is 7 cm, calculate its height.
[Take π = ]
2.0 cm
4.0 cm
4.5 cm
7.5 cm
23.
If 2a = and = 3, evaluate a2 + b2.
48
90
160
250
24.
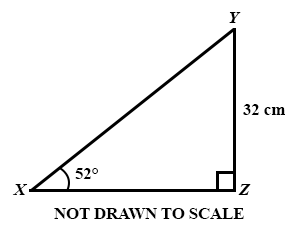
In ∆XYZ, |YZ| = 32 cm, ∠ YXZ = 52° and ∠ XZY = 90°. Find, correct to the nearest centimetre, |XZ|.
13 cm
20 cm
25 cm
31 cm
25.
If logx2 = 0.3, evaluate logx8.
0.6
0.9
1.2
2.4
26.
An arc subtends an angle of 72° at the center of the circle. Find the length if the radius of the circle is 3.5 cm.
[Take π = ]
2.2 cm
4.4 cm
8.8 cm
6.6 cm
27.
Make b the subject of the relation lb = (a + b)h.
28.
Eric sold his house through an agent who charged 8% commission on the selling price. If Eric received $117,760.00 after the sale, what was the selling price of the house?
$120,000.00
$125,000.00
$128,000.00
$130,000.00
29.
Find the angle which an arc of length 22 cm subtends at the centre of a circle of radius 15 cm.
[Take π = ]
156°
96°
84°
70°
30.
A rectangular board has length 15 cm and width x cm. If the sides are doubled, find its new area.
15x cm2
30x cm2
45x cm2
60x cm2
31.
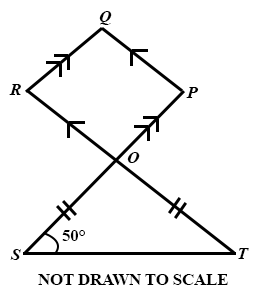
In the diagram, POS and ROT are straight lines. OPQR is a parallelogram, |OS| = |OT| and ∠ OST = 50°. Calculate the value of ∠ OPQ.
160°
140°
120°
100°
32.
Factorize completely: (2x + 2y)(x - y) + (2x - 2y)(x + y).
2(x - y)
2(x - y)(x + y)
4(x - y)
4(x - y)(x + y)
33.
The interiors angle of a polygon are 3x°, 2x°, 4x°, 3x° and 6x°. Find the size of the smallest angle of the polygon.
30°
40°
60°
80°
34.
A box contains 2 white and 3 blue identical balls. If two balls are picked at random from the box, one after the other with replacement, what is the probability that they are of different colours.
35.
Find the equation of a straight line passing through the point (1,-5) and having gradient of .
3x - 4y - 23 = 0
3x - 4y + 23 = 0
3x + 4y + 23 = 0
3x + 4y - 23 = 0
36.
The foot of a ladder is 6 m from the base of an electric pole. The top of the ladder rests against the pole at a point 8 m above the ground. How long is the ladder?
7 m
10 m
12 m
14 m
37.
If tan x = , 0 < x < 90, evaluate
38.
From the top of a vertical cliff 20 m high, a boat at sea can be sighted 75 m away and on the same horizontal position as the foot of the cliff.
Calculate, correct to the nearest degree, the angle of depression of the boat from the top of the cliff.
15°
16°
75°
56°
39.
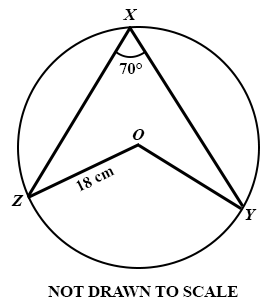
In the diagram, O is the centre of the circle with radius 18 cm. If the angle ∠ ZXY = 70°, calculate the length of arc ZY.
[Take π = ]
80 cm
44 cm
22 cm
11 cm
40.
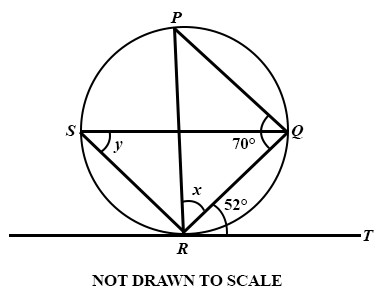
In the diagram, RT is a tangent to the circle at R, ∠ PQR = 70°, ∠ QRT = 52°, ∠ QSR = y and ∠ PRQ = x.
Use the diagram to answer the question below.
Find the value of y.
18°
52°
60°
45°
41.

In the diagram, RT is a tangent to the circle at R, ∠ PQR = 70°, ∠ QRT = 52°, ∠ QSR = y and ∠ PRQ = x.
Use the diagram to answer the question below.
Calculate the value of x.
48°
55°
58°
70°
42.
Calculate the variance of 2, 4, 7, 8 and 9.
2.6
3.5
6.8
7.2
43.
The fourth term of an Arithmetic Progression (A.P) is 37 and the first term is -20. Find the common difference.
17
19
57
63
44.
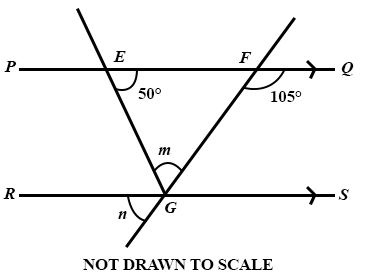
In the diagram PQ is parallel to RS, ∠ QFG = 105° and ∠ FEG = 50°.
Use the diagram to answer the question below
Find the value of m.
55°
75°
105°
130°
45.

In the diagram PQ is parallel to RS, ∠ QFG = 105° and ∠ FEG = 50°.
Use the diagram to answer the question below
Find the value of n.
130°
75°
55°
40°
46.
A box contains 5 red, 6 green and 7 yellow pencils of the same size. What is the probability of picking a green pencil at random?
47.
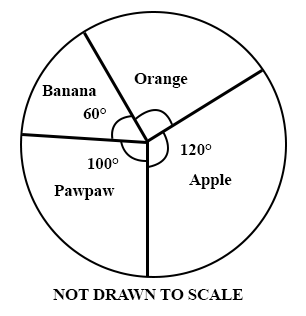
The pie chart represents fruits on display in a grocery shop. If there are 60 oranges on display, how many apples are there?
40
80
90
70
48.
The following are scores obtained by some students in a test:
| 8 | 18 | 10 | 14 | 18 | 11 | 13 |
| 14 | 13 | 17 | 15 | 8 | 16 | 13 |
Use this information to answer the question below
Find the mode of the distribution.
8
13
14
18
49.
The following are scores obtained by some students in a test:
| 8 | 18 | 10 | 14 | 18 | 11 | 13 |
| 14 | 13 | 17 | 15 | 8 | 16 | 13 |
Use this information to answer the question below
Find the median score.
13.0
13.5
14.0
14.5
50.
The following are scores obtained by some students in a test:
| 8 | 18 | 10 | 14 | 18 | 11 | 13 |
| 14 | 13 | 17 | 15 | 8 | 16 | 13 |
Use this information to answer the question below
How many students scored above the mean score?
7
8
9
10
(a)
Without using mathematical tables or calculators, evaluate , leaving the answer in standard form.
(b)
If = , find, correct to two decimal places, the value of .
(a)
Z varies directly as x and inversely as twice the cube root of y.
If Z = 8, when x = 4 and y = , find the relation for y in terms of x and Z.
(b)
Factorize completely: 4b2 - ab + (a + 9b)2 - a2.
(a)
Solve + = -
(b)
Evaluate +
A car dealer made a profit of 22.5% by selling a car for GH₵ 58,000.00. Find, correct to two decimal places, the percentage profit if the car had been sold for GH₵ 61,200.00
(a)
A number is chosen at random from Q = {1, 2, 3, ....,10}
Find the probability that the chosen number is either a prime factor of 42 or a multiple of 3.
(b)
If 110x = 1020four, find the value of x.
(a)
If a = , b = and r = a + (a - b), find:
(i)
r;
(ii)
|r|
(b)
Given that a = bc and n = ,
(i)
express k in terms of a, b, e, m and n;
(ii)
find, correct to three significant figures, the value of k, when a = , b = -4, e = 3, m = 7 and n = -5.
(a)
Copy and complete the table of values for y = 5sin x + 9cos x for 0° ≤ x ≤ 150°.
| x | 0° | 30° | 60° | 90° | 120° | 150° |
| y | 10.3 | -0.2 |
(b)
Using a scale of 2 cm to 30° on the x-axis and 2 cm to 2 units on the y-axis, draw the graph of y = 5sin x + 9cos x for 0° ≤ x ≤ 150°.
(c)
Use the graph to solve the equations:
(i)
5sin x + 9cos x = 0;
(ii)
5sin x + 9cos x = 2.
(d)
Using the graph, find, the value of y when x = 45°.
(a)
Using ruler and a pair of compasses only, construct:
(i)
the quadrilateral ABCD such that |AB| = 6.5 cm, |BC| = 9 cm, |AD| = 4 cm, ∠ ABC = 60° and ∠ BAD = 120°;
(ii)
the perpendicular bisectors of BC and CD.
(b)
Locate the point of intersection, T, of the two bisectors in (a(ii).
(c)
With the point T in (b) as centre, draw a circle to pass through the vertices B, C and D.
(d)
Measure:
(i)
|BT|;
(ii)
|CD|.
(a)
Using a scale of 2 cm to 1 unit on both axes, draw on a sheet of graph paper, two perpendicular axes 0x and 0y for – 5 ≤ x ≤ 5 and – 5 ≤ y ≤ 5.
(b)
Draw on the same graph sheet, indicating clearly all vertices and their coordinates:
(i)
∆ ABC with vertices A(2, 1), B(1, 4) and C(–1, 2);
(ii)
the image ∆ A1B1C1 of ∆ ABC under a reflection in the line y = 0, where A→A1, B→B1 and C→C1;
(iii)
the image ∆ A2B2C2 of ∆ ABC under a translation by the vector , where A→A2,B→B2 and C→C2;
(iv)
the image ∆ A3B3C3 of ∆ ABC under an anticlockwise rotation of 90° about the origin, where A→A3, B→B3 and C→C3.
(c)
What single transformation maps ∆ A1B1C1 onto ∆ A3B3C3, where A1→A3, B1→B3 and C1→C3?
(a)
In a class of 50 students, 24 like football, 21 basketball and 18 crickets. 6 like football and basketball only, 3 like basketball only, 5 like all the three games and 14 did not like any of the three games.
(i)
Illustrate this information on a Venn diagram.
(ii)
Find the number of students who like:
(α)
football and cricket only;
(β)
exactly one of the games.
(b)
If (3 - a), 6, (7 - 5a) are consecutive terms of a Geometric Progression (G.P) with common ratio r > 0, find the values of a.
(a)
Two passenger trains, A and B, 450 km apart, start to move towards each other at the same time and meet after 2 hours. If train B, travels as fast as train A.
Find the speed of each train.
(b)
A solid cube of side 8 cm was melted to form a solid circular cone. The base radius of the cone is 4 cm. Calculate, correct to one decimal place, the height of the cone.
[Take π = ]
(a)
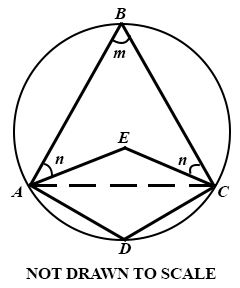
The diagram shows a circle ABCD with centre E. Quadrilateral EADC is a rhombus, ∠ BAE = ∠ ECB = n and ∠ ABC = m.
Find:
(i)
m;
(ii)
n.
(b)
Find the quadratic equation whose roots are and -4.
(a)
The fourth term of an Arithmetic Progression (A.P) is one less than twce the second term. If the sixth term is 7, find the first term.
(b)
A clerk spends , and of his annual salary on rent, transport and entertainment respectively.
If after all these expenses he had GH₵ 4,100.00 left, find how much he earns per annum.
(c)
Given that f : x → 2x2 - 8x + 5 and g : x → x - 2;
Find:
(i)
f(-3);
(ii)
the values of x such that f(x) = g(x).