1.
Evaluate, correct to two decimal places, 75.0785 - 34.624 + 9.83.
30.62
50.28
50.29
30.60
2.
If X = {x:x < 7} and Y = {y:y is a factor of 24} are subsets of µ = {1, 2, 3, ......, 10}, find X ∩ Y.
{1, 2, 3, 4, 6, 8}
{2, 3, 4, 6, 8}
{1, 2, 3, 4, 6}
{2, 3, 4, 6}
3.
Simplify:
4.
Find the least value of x which satisfies the equation 4x = 7 (mod 9)
4
5
6
7
5.
Express 1 + 2 log103 in the form log10q
log106
log109
log1019
log1090
6.
If 101two + 12y = 23five, find the value of y.
5
6
7
8
7.
An amount of ₦ 550,000.00 was realized when a principal, x was saved at 2% simple interest for 5 years. Find the value of x.
₦ 500,000.00
₦ 490,000.00
₦ 480,000.00
₦ 470,000.00
8.
Given that = x + y, find the value of (x + y)
1
1
1
9.
If x = 3 and y = -1, evaluate 2(x2 - y3).
16
20
22
24
10.
Solve 3x - 2y = 10 and x + 3y = 7.
x = 4, y = 1
x = 1, y = 4
x = -1, y = -4
x = -4, y = 1
11.
The implication x ⇒ y is equivalent to
~ y ⇒ ~ x.
y ⇒ ~ x.
~ x ⇒ ~ y.
y ⇒ x.
12.
The first of a Geometric Progression (G.P) is 3 and the 5th term is 48. Find the common ratio.
16
8
4
2
13.
Solve: (5 - 3x) < (3 - 7x).
x <
x >
x <
x >
14.
Make m the subject of the relation k = .
m =
m =
m =
m =
15.
Find the quadratic equation whose roots are and -.
6x2 - x - 1 = 0
3x2 + x - 1 = 0
6x2 + x - 1 = 0
3x2 + x + 1 = 0
16.
Given that x is directly proportional to y and inversely proportional to z, x = 15 when y = 10 and z = 4, find the equation connecting x, y and z.
x =
x =
x =
x =
17.
Two buses start from the same station at 9.00 am and travel in opposite directions along the same straight road. The first bus travels at a speed of 72 km/h and the second at 48 km/h.
At what time will they be 240 km apart?
10.00 a.m.
11.00 a.m.
12.00 noon
1.00 p.m.
18.
A solid cuboid has length 7 cm, width 5 cm and height 4 cm. Calculate its total surface area.
83 cm2
140 cm2
166 cm2
280 cm2
19.
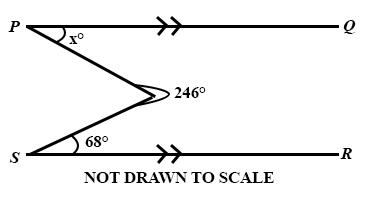
In the diagram, PQ//SR. Find the value of x.
68
57
46
34
20.
Find the equation of the line parallel to 2y = 3(x - 2) and passes through the point (2, 3).
y = x
y = x
y = x - 2
y = x - 3
21.
The expresson will be undefined when x equals
{-3, 0}.
{-3, -1}.
{0, -1).
{0, 1}.
22.
A man is five times as old as his son. In four years time, the product of their ages would be 340. If the son's age is y, express the product of their ages in terms of y.
5y2 + 24y - 324 = 0
5y2 - 16y - 330 = 0
5y2 + 24y - 308 = 0
5y2 - 16y - 380 = 0
23.
Simplify: - - .
24.
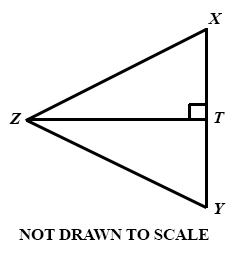
In the diagram, XZY is an equilateral triangle of side 6 cm and T is the midpoint of XY.
Find tan (∠ XZT).
25.
A fence 2.4 m tall, is 10 m away from a tree of height 16 m. Calculate the angle of elevation of the top of the tree from the top of the fence.
51.32°
52.40°
53.67°
76.11°
26.
Fati buys milk at ₦ x per tin and sells each at a profit of ₦ y. If she sells 10 tins of milk, how much does she receive from the sales?
₦ 10(x + y)
₦ (10x + y)
₦ (x + 10y)
₦ (xy + 10)
27.
If tan y is positive and sin y is negative, in which quadrant would y lie?
Second only
Third only
First and second only
First and third only
28.
The dimensions of a rectangular base of a right pyramid are 9 cm by 5 cm. If the volume of the pyramid iis 105 cm3, how high is the pyramid?
7 cm
8 cm
6 cm
10 cm
29.
Each interior angle of a regular polygon is 168°. Find the number of sides of the polygon.
18
24
36
30
30.
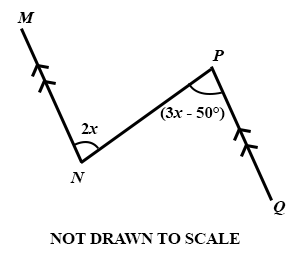
In the diagram, MN//PQ, ∠ MNP = 2x and ∠ NPQ = (3x - 50°). Find the value of ∠ NPQ.
100°
120°
150°
200°
31.
The length of an arc of a circle of radius 3.5 cm is 1 cm. Calculate, correct to the nearest degree, the angle subtended by the arc at the centre of the circle.
[Take π = ]
22°
25°
36°
55°
32.
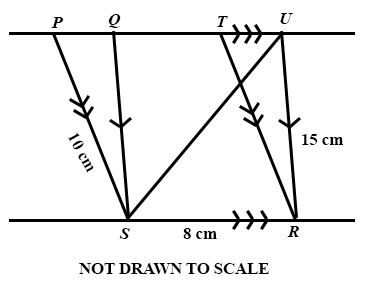
In the diagram, PU//SR, PS//TR, QS//UR. |UR| = 15 cm, |SR| = 8 cm, |PS| = 10 cm and area of ∆SUR = 24 cm2. Calculate the area of PTRS.
120 cm2
80 cm2
48 cm2
40 cm2
33.
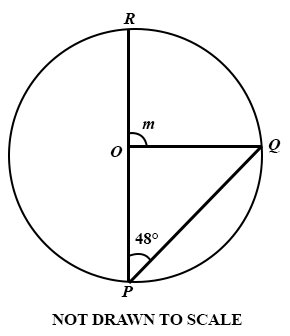
In the diagram, PQR is a circle with centre O. If ∠ OPQ = 48°, find the value of m.
42°
68°
90°
96°
34.
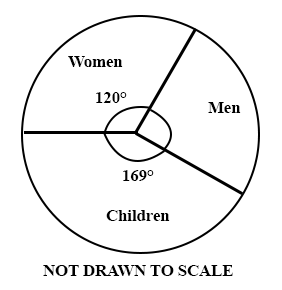
The pie chart shows the population of men, women and children in a city. If the population of the city is 1,800,000, how many men are there?
250,000
355,000
600,000
845,000
35.
The mean of the numbers 15, 21, 17, 26, 18 and 29 is 21. Calculate the standard deviation.
0
5
6
9
36.
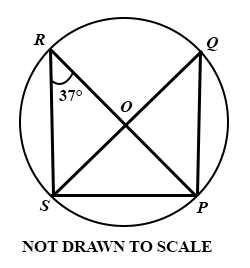
In the diagram, O is the centre of the circle. SOQ is a diameter and ∠ SRP = 37°.
Find ∠ PSQ.
37°
53°
65°
127°
39.
A box contains 12 identical balls, of which 5 are red, 4 blue and the rest are green.
Use this information to answer the question below
If a ball is selected at random from the box, what is the probability that it is green?
40.
A box contains 12 identical balls, of which 5 are red, 4 blue and the rest are green.
Use this information to answer the question below
If two balls are selected at random one after the other with replacement, what is the probability that both are red?
41.
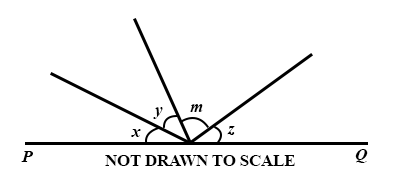
In the diagram, PQ is a straight line. If m = (x + y + z), find the value of m.
100°
90°
60°
45°
42.
| x | 6.20 | 6.85 | 7.5 |
| y | 3.9 | 5.2 | 6.5 |
The points on a linear graph are as shown in the table. Find the gradient (slope) of the line.
1
2
2
43.

In the diagram, O is the centre of the circle, PQ and RS are tangents to the circle.
Find the value of (m + n).
60°
75°
90°
120°
44.
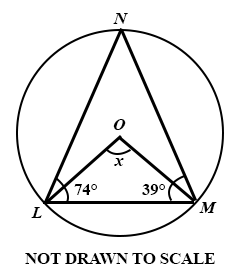
In the diagram, O is the centre of the circle. If ∠ NLM = 74°, ∠ LMN = 39° and ∠ LOM = x, find the value of x.
106°
113°
126°
134°
45.
Which of the following is not a sufficient condition for two triangles to be congruent?
AAS
SSS
SAS
SSA
46.
A woman received a discount of 20% on a piece of cloth she purchased from a shop. If she paid $ 525.00, what was the original price?
$616.25
$656.25
$660.25
$675.25
47.
The interquartile range of a distribution is 7. If the 25th percentile is 16, find the upper quartile.
9
23
30
35
48.
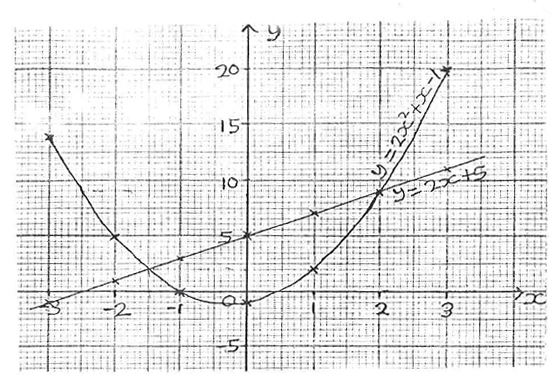
The graphs of the equations y = 2x + 5 and y = 2x2 + x - 1 are shown.
Use the information to answer the question below
Find the points of intersection of the two graphs.
(2.0, 7.5) and (-1.5, 2.5)
(2.0, 8.0) and (-1.5, 2.5)
(2.0, 8.5) and (-1.5, 2.0)
(2.0, 9.0) and (-1.5, 2.0)
49.

The graphs of the equations y = 2x + 5 and y = 2x2 + x - 1 are shown.
Use the information to answer the question below
If x = -2.5, what is the value of y on the curve?
y = 9.5
y = 9.0
y = 8.5
y = 8.0
50.
If (x + 2) is a factor of x2 + px - 10, find the value of p.
-7
7
-3
3
(a)
In a small town, 68% of the people owned Television, 72% owned Radio and 12% owned neither Television nor Radio.
(i)
Represent the information on a Venn diagram.
(ii)
What percentage of the population owned Television only?
(b)
Boadu and Ansah formed a company and agreed that their annual profit will be shared in the ratio 4 : 5 respectively. If at the end of the year, Ansah received GH₵ 5,00.00 more than Boadu, how much was Boadu's share?
(a)
Make y the subject of the relation: p = 2x
(b)
Given that m = 3, n = -2 and x = -1, evaluate
(a)
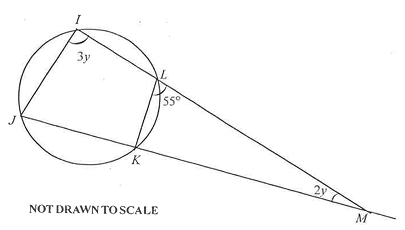
In the diagram IJKL are points on a circle such that ∠ JIL = 3y and ∠ KML = 2y.
If ∠ KLM = 55°, find the value of y.
(b)
Given that tan x = 1, 0° ≤ x ≤ 90°, evaluate .
(a)
A cone and a pyramid have equal heights and volumes. If the base area of the pyramid is 154 cm2, find the radius of the cone.
[Take π = ]
(b)
A spherical bowl of radius r cm is a quarter full when 6 litres of water is poured into it.
Calculate, correct to three significant figures, the diameter of the bowl.
[Take π = ]
| Class | JHS 1 | JHS 2 | JHS 3 |
| Boys | 32 | 26 | 26 |
| Girls | 28 | 44 | 36 |
The table above shows three classes: JHS 1, JHS 2 and JHS 3 in a school. The three classes were combined to select a prefect.
What is the probability that the prefect will be:
(a)
a boy?
(b)
a girl in JHS 2?
(a)
Copy and complete the table of values for the relation y = 7cos x - 3sin x.
| x | 0° | 30° | 60° | 90° | 120° | 150° |
| y | 7.0 | -3.0 |
(b)
Using a scale of 2 cm to 30° on the x-axis and a scale of 2 cm to 2 units on the y-axis, draw the graph of y = 7cos x - 3sin x for 0° ≤ x ≤ 150°.
(c)
Use the graph to solve the equations:
(i)
7cos x = 3sin x;
(ii)
7cos x = 3.2 + 3sin x.
(a)
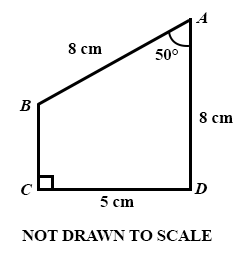
In the diagram |AB| = |AD| = 8 cm and |CD| = 5 cm. If ∠ BCD = 90° and ∠ BAD = 50°, calculate, correct to the nearest whole number:
(i)
|BD|;
(ii)
the area of ∆BCD.
(b)
A man is five times as old as his son. In three years time, the product of their ages will be 380. Find their present ages.
(a)
A market woman purchased a number of plates for GH₵ 150.00. Four of the plates got broken while transporting them to her shop.
By selling the remaining plates at a profit of GH₵ 1.00 on each, she made a total profit of GH₵ 6.00.
How many plates did she purchase?
(b)
If , m, , n, ...... are in Geometric Progression (G.P), find the values of m and n.
(a)
Two points X and Y, 7 metres apart are on the same horizontal ground. The angles of elevation of a point P from X and Y are 50° and 70° respectively.
Q is a point on XY produced such that ∠ YQP = 90°.
(i)
Illustrate the information in a diagram.
(ii)
Calculate, correct to two decimal places, the length:
(α)
XP;
(β)
YQ.
(b)
Solve the equation: + = 2.
The table shows the age distribution of workers in a company.
| Age (years) | 26 - 30 | 31 - 35 | 36 - 40 | 41 - 45 | 46 - 50 | 51 - 55 | 56 - 60 |
| Number of workers | 11 | 24 | 29 | 15 | 10 | 9 | 2 |
(a)
Construct a cumulative frequency table and use it to draw a cumulative frequency curve.
(b)
Use the curve to estimate the:
(i)
probability of selecting a worker whose age is not more than 45 years;
(ii)
number of workers who will retire if the retiring age is 50 years and above.
(a)
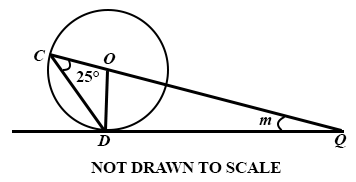
The diagram shows a circle, centre O, with C and D as points on the circumference.
DQ is a tangent produced at Q.
Find the value of m.
(b)
Find the equation of the line which has the same gradient (slope) as 2y + x = 6 and passes through the point (-2, 3).
(c)
The ratio of the profit, labour and cost of materials in the production of an article is 5 : 7 : 13 respectively.
If the cost of materials is Le 840 more than that of labour, find the total cost of producing the article.
(a)
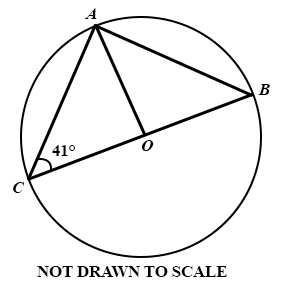
In the diagram, O is the centre of the circle ABC and ∠ BCA = 41°.
Find:
(i)
∠ BOA;
(ii)
∠ BAO.
(b)
The angle of depression of a point P on the ground from the top, T, of a building is 23.6°.
If the horizontal distance from P to the base of the building is 50 m, calculate, correct to three significant figures, the height of the building.
(c)
A cow is tied to a post at the centre of a square grazing field of side 25 m by a rope 10 m long.
Find, correct to two decimal places the percentage of the field the cow is able to graze on.
[Take π = ]
(a)
Given that f : x → x + 3 and g : x → x2.
(i)
find g(f(x)),
(ii)
evaluate g(f(2)).
(b)
Find what values of x is + undefined?
(c)
Given that f(x) = + and f(5) = 8, find the value of k.