1.
Correct 0.00798516 to three significant figures.
0.0109
0.0800
0.00799
0.008
2.
Simplify: (11two)2
1001two
1101two
101two
10001two
3.
Solve: = 32
13
24
12
11
4.
If log10 2 = m and log10 3 = n, find log10 24 in terms of m and n.
3m + n
m + 3n
4mn
3mn
5.
Find the 5th term of the sequence 2, 5, 10, 17....?
22
24
36
26
6.
If P = {-3 < x < 1} and Q = {-1 < x <3}, where x is a real number, find P ∩ Q.
{-1 ≤ x ≤ 1}
{-3 < x < 1}
{-3 ≤ x ≤ 1}
{-1 < x < 1}
7.
Factorize 6pq - 3rs - 3ps + 6qr.
3(r - p)(s - 2q)
3(r - p)(2q + s)
3(p - r)(2q - s)
3(p + r)(2q - s)
8.
What number should be subtracted from the sum of 2 and 2 to give 3?
1
1
9.
Mensah is 5 years old and Joyce is thrice as old as Mensah. In how many years will Joyce be twice as old as Mensah?
3 years
10 years
5 years
15 years
10.
If 16 x 2(x + 1) = 4x x 8(1 − x), find the value of x.
-4
4
1
-1
11.
The circumference of a circular track is 9 km. A cyclist rides round it a number of times and stops after covering a distance of 302 km. How far is the cyclist from the starting point?
5 km
6 km
7 km
3 km
12.
Simplify: 2 - +
3
13.
If 4x + 2y = 16 and 6x -2y = 4, find the value of (y - x).
8
2
4
6
14.
Given that R is directly proportional to L and inversely proportional to P, R = 3 when L = 9 and P = 0.8, find R when L = 15 and P = 1.8.
0.3
2.2
3.3
6.6
15.
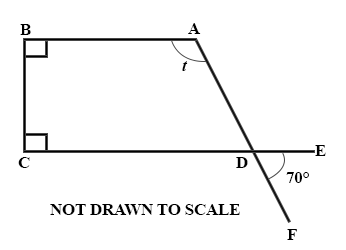
In the diagram, ∠ABC and ∠BCD are right angles, ∠BAD = t and ∠EDF = 70°. Find the value of t.
70°
165°
140°
110°
16.
The sum of the interior angles of a regular polygon with k sides is (3k - 10) right angles.
Find the size of the exterior angle.
60°
40°
90°
120°
17.
Make U the subject of the relation: x = .
U =
U =
U =
U =
18.
A trader paid import duty of 38 kobo in the naira on the cost of an engine. If a total of ₦ 22,800.00 was paid as import duty, calculate the cost of the engine.
₦60,000.00
₦120,000.00
₦24,000.00
₦18,000.00
19.
The height of an equilateral triangle is 10 cm.
Calculate its perimeter.
20 cm
60 cm
40 cm
30 cm
20.
In a △LMN, |LM| = 6 cm, ∠LMN = 90°, ∠LNM = x and sin x = .
Find the area of △LMN.
60 cm2
48 cm2
24 cm2
30 cm2
21.
Consider the statements:
P: = All students offering Literature(L) also offer History(H);
Q: = Students offering History(H) do not offer Geography(G).
Which of the Venn diagram correctly illustrate the two statements?
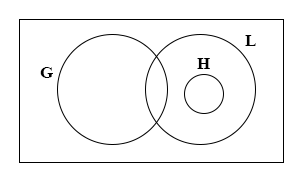
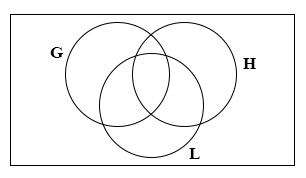
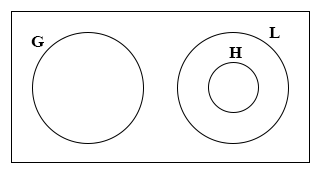
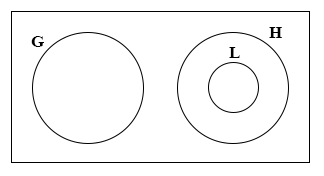
22.
Find The quadratic Equation whose roots are -2q And 5q.
x2 + 3qx + 10q2
x2 - 3qx + 10q2
x2 - 3qx - 10q2
3x2 + 3qx - 10q2
23.
If tan θ = , 180° < θ < 270°, find the value of cos θ.
-
-
24.
If - = , find p.
-(5x - 13)
(13 - x)
(5 - x)
-(x + 5)
25.
The diagonal of a rhombus are 12 cm and 5 cm.
Calculate its perimeter.
26 cm
24 cm
17 cm
34 cm
26.
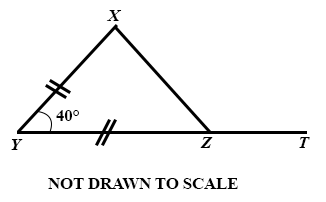
In the diagram, △XYZ is produced to T. If |XY| = |ZY| and ∠XYT = 40°, find ∠XZT.
110°
130°
140°
180°
27.
A solid brass cube is melted and recast as a solid cone of height h and base radius r. If the height of the cube is h, find r in terms of h.
r =
r = πh
r = h
r = h
28.
Which of the following is not an exterior angle of a regular polygon?
66°
72°
24°
15°
29.
From a point T, a man moves 12 km due West and then moves 12 km due South to another point Q.
Calculate the bearing of T from Q.
225°
315°
045°
135°
30.
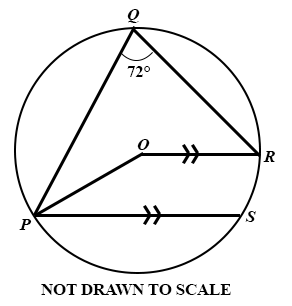
In the diagram, O is the centre of the circle PQRS, ∠PQR = 72° and OR//PS. Find ∠ OPS.
18°
108°
54°
36°
31.
A trapezium of parallel sides 10 cm and 21 cm and height 8 cm is inscribed in a circle of radius 7 cm.
Calculate the area of the region not covered by the trapezium.
[Take π = ]
84 cm2
80 cm2
30 cm2
94 cm2
32.
Find correct to two decimal places the mean of 1, 2, 3, 4 and 5
3.72
3.71
3.70
3.69
33.
A cyclist moved at a speed of X km/h for 2 hours. He then increased his speed by 2 km/h for the next 3 hours.
If the total distance covered is 36 km, calculate his initials speed.
12 km/h
3 km/h
4 km/h
6 km/h
34.
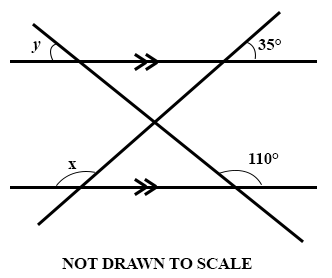
Find the value of (x + y) in the diagram.
215°
145°
135°
70°
35.
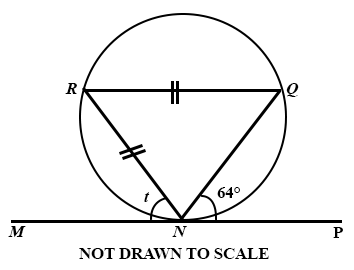
In the diagram, MP is a tangent to the circle NQR, ∠ PNQ = 64° and |RQ| = |RN|.
Find the angle marked t.
58°
68°
115°
130°
36.
Find the first quartile of 7, 8, 7, 9, 11, 8, 7, 9, 6 and 8.
8.5
7.0
7.5
8.0
37.
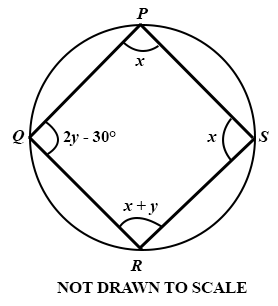
In the diagram, PQRS is a circle. find the value of x.
50°
30°
80°
100°
38.
A cone has a base radius of 8 cm and height 11 cm.
Calculate , correct to two decimal places, the curved surface area.
[Take π = ]
341.98 cm2
276.57 cm2
201.14 cm2
477.71 cm2
39.
Given that sin x = , 0° ≤ x ≤ 90°, evaluate (tan x + 2 cos x).
1
2
40.
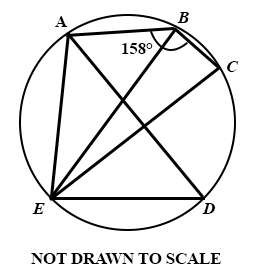
In the diagram EC is a diameter of circle ABCDE. If ∠ ABC = 158°, find ∠ ADE.
22°
112°
90°
68°
41.
| Height (cm) | 160 | 161 | 162 | 163 | 164 | 165 |
| Number of players | 4 | 6 | 3 | 7 | 8 | 9 |
The table shows the heights of thirty-seven players of a basketball team.
Calculate, correct to one decimal place, the mean height of the players.
165.0
163.0
162.0
160.0
42.
XY is a line segment with the coordinates X(-8, -12) and Y(p, q). If the midpoint of XY is (-4, -2), find the coordinates of Y.
(0, 4)
(4, 10)
(-6, -10)
(0, 8)
43.
Five hundred tickets were sold for a concert. Tickets for adults and children were sold at $4.50 and $3.00, respectively.
If the total receipts for the concerts was $1987.50, how many tickets for adults were sold?
325
235
175
400
44.
The distance (d) between two villages is more than 18 km but not more than 23 km.
Which of these inequalities represents the statements?
18 ≤ d ≤ 23
18 < d < 23
18 ≤ d < 23
18 < d ≤ 23
45.
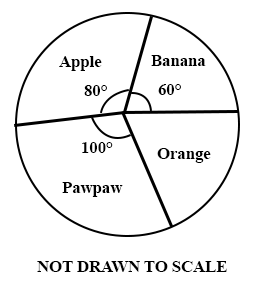
The pie chart represents the distribution of fruits on display in a shop. If there are 60 apples on display, how many oranges are there?
80
270
120
90
46.
A box contains 40 identical balls of which 10 are red and 12 are blue. If a ball is selected at random from the box, what is the probability that it is neither red nor blue?
47.
A fair die is tossed twice. What is the probability of getting a sum of at least 10?
48.
A man will be (x + 10) years old in 8 years time. If 2 years ago he was 63 years, find the value of x
55
63
57
67
49.
The equation of a line is given as 3x - 5y = 7. Find its gradient (slope).
-
-
50.
For what value of x is undefined?
-2
-1
1
2
(a)
(i)
Draw the multiplication ⊗ table in modulo 9 on {2, 3, 7, 8}.
(ii)
Use the table to find the truth set of 8 ⊗ m = 2
(b)
Consider the following statements:
X: All policemen wear uniform;
Y: Civil servants do not wear uniform.
If P = {policemen}, T = {people who wear uniform} and C = {civil servants},
(i)
draw a Venn diagram to illustrate X and Y;
(ii)
use the venn diagram to determine which of the following implications are valid or not valid conclusions from X and Y;
(α)
Adu wears uniform ⇒ Adu is a policeman;
(β)
Ofei is a policeman ⇒ Ofei is not a Civil Servant
(a)
Given that p = ,
(i)
Make t the subject of the relation.
(ii)
Find the value of t when p = and q = .
(b)
Given that m = and n = , express, in simplest form, (2m - n) in terms of x.
(a)
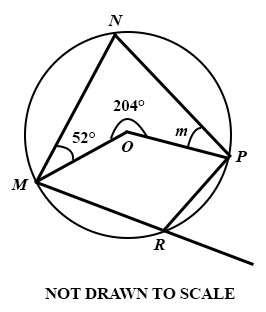
In the diagram is a circle MNPR with centre O. The reflex angle at O is 204°, ∠ NMO = 52°.
Find the value of m.
(b)
A ladder of length 6.5 m leans against a vertical wall. If the top of the ladder is 3.6 m from the foot of the wall, calculator, correct to two decimal places, the distance from the wall to the foot of the ladder.
(a)
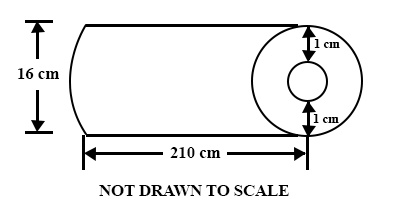
The diagram is a cylindrical pipe with length 210 cm. It has external diameter of 16 cm and is 1 cm thick.
Find the volume of the metal used in constructing the pipe.
[Take π = ]
(b)
The coordinates of the points M and N are (5, -7) and (0, 5), respectively.
Calculate the distance between M and N.
Two dice are thrown together once. Find the probability of obtaining:
(a)
an odd number on the first die and 6 on the second;
(b)
a number greater than 4 on each dice;
(c)
a total of 9 or 11.
In a military camp, 50 officers had a choice of beans, plantain and rice. Of these officers, 21 chose beans, 24 plantains and 18 rice. Also 3 chose beans only, 9 plantain only, 2 rice only and 5 chose all three kinds of food.
(a)
Illustrate the information on a Venn diagram.
(b)
Use the Venn diagram to find the number of officers who chose:
(i)
plantain and beans only;
(ii)
exactly two kinds of food;
(iii)
none of the three kinds of food.
(a)
Copy and complete the table of values for the relation y = 4 + 3x - 2x2, for -4 ≤ x ≤ 4.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -10 | 4 | 2 |
(b)
Using a scale of 2 cm to 1 unit on the x – axis and 2 cm to 5 units on the y – axis, draw the graph for the relation y = 4 + 3x - 2x2, for -4 ≤ x ≤ 4.
(c)
Using the graph, find the:
(i)
equation of line of symmetry of the curve;
(ii)
maximum point of the curve;
(iii)
values of x for which y decreases as x increases.
(a)
A solid metal cylinder of height 6 m and diameter 28 cm is melted and recast into smaller solid cylinders. Each of the smaller cylinders is 14 cm high and 0.5 cm in diameter.
How many smaller cylinders were obtained?
[Take π = ]
(b)
The unit digit of a two digit number is 1 less than the tens digit. If the number is increased by 8 and then divided by the sum of the digits, the results is 8. Find the number.
(a)
The ratio of cars to motorcycles sold at a garage is 5 : 7. If a dealer sold 142 more motorcycles than cars in a particular month, find the number of each type of vehicle sold.
(b)
The probabilities of an athlete winning two independent events are and .
Find the probabilities of winning:
(i)
only one event;
(ii)
none of the events.
(a)
A cyclist sets out from a town P on the bearing of 060° to a town Q, 5 km away.
He then moves on the bearing of 345° to a town R, 6 km from Q.
(i)
Represent the information on a diagram.
(ii)
Calculate, correct to two decimal places
(α)
|PR|
(β)
the bearing of R from P.
(b)
The following are arranged in order of size: (x – 2), 4, (x + 2), (2x + 1) and 9.
If the median is equal to the mean, find the value of x
(a)
The average mass of refuse generated in a community in a week contains 35% plastic, 27.5% liquid, 17.5% metal, 12.5% vegetable matter and others 7.5%. Draw a pie chart to illustrate the information.
(b)
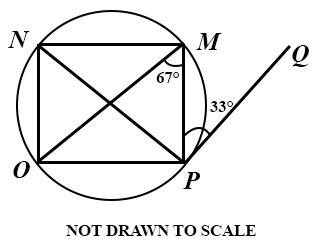
In the diagram PQ touches the circle MNOP at P and NP is a diameter. ∠ MPQ = 33° and ∠ PMO = 67°
Find:
(i)
∠ MNO;
(ii)
∠ MPO.
(a)
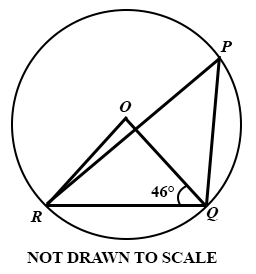
In the diagram, PQR is a circle with centre O. If ∠ RQO = 46°, find ∠ RPQ.
(b)
A train is scheduled to cover a distance of 120 km at a certain average speed, r. Due to some technical challenges the average speed is reduced by 5 km/h thereby increasing the scheduled time by 20 minutes. Find the average speed, r.
(a)
A function g is defined on the set of real numbers, R, by g(x) = , x ≠ 1.
Find the:
(i)
image of - 1 under the function g;
(ii)
value for x for which g(x) = 7
(ii)
value of g(-3).
(b)
The sum of the first ten terms of an Arithmetic Progression (A.P.) is 120.
If the fifth term is 6 less than the eighth term, find the:
(i)
common difference;
(ii)
first term.