1.
Find the number of even integers between 11 and 97.
43
44
45
53
2.
Find the values of x for which is not defined.
5,
1,
2, 15
13, 15
3.
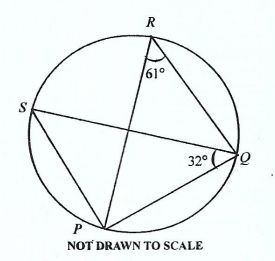
In the diagram P,Q,R,S are points on the circle. If ∠PQS = 32o and ∠PRQ = 61o, find ∠QPS.
32o
61o
87o
93o
4.
The bearing of a point P from a point Q is 065o. What is the bearing of Q from P?
115o
155o
245o
295o
5.
The arc of a circle 50 cm long subtends an angle 75o at the centre of the circle.
Find, correct to three significant figures, the radius of the circle.
[Take π = ]
76.4 cm
61.2 cm
38.2 cm
8.74 cm
6.
Find the truth set of (3 + x)(1 - x) > 9 - x2.
{x:x > 3}
{x:x > -3}
{x:x < 3}
{x:x < -3}
7.
A bag contains 32 blue, 28 black and 20 red identical balls of same size. If a ball is picked at random, what is the probability that it is not red?
8.
Simplify: (x-1)-(x-1).
(x-1)
(2x+1)
(2x-1)
(1-2x)
9.
A woman buys 3 exercise books at GH₵ 0.4 each and 9 exercise books at GH₵ 0.2 each. What is the average cost of an exercise book?
GH₵ 0.35
GH₵ 0.30
GH₵ 0.22
GH₵ 0.25
10.
Given that 4x + 6y = 5 and 2x + 4y = 3, find the value of (x + 2y)
-1
-1
1
1
11.
Simplify , where x ≠ 3
12.
Given that P ∝ and x ∝ vt express P in terms of v and t.
P ∝
P ∝
P ∝ vt
P ∝
13.
Express, correct to two significant figures ( - ).
0.036
0.035
0.030
0.040
14.
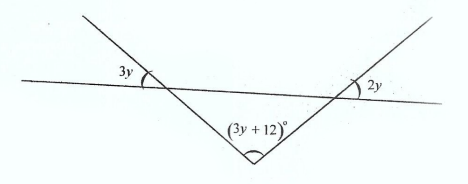
Find the value of y in the diagram.
30o
21o
20o
10o
15.
If 23x = 1111two, find the value of x.
5
6
7
8
16.
Dina and Rose were given GH₵ 875.08 to be shared in the ratio 3:2 respectively. If Rose shared her part of the money between Efua and Ama in the ratio 1:2 respectively, how much was Ama's share?
GH₵ 116.68
GH₵ 175.02
GH₵ 233.35
GH₵ 340.32
17.
If 9 y + 1 = () y - 2, find y.
-
1
-4
18.
A market woman demands GH₵ 15.00 for a tin of local rice. After some bargaining with a customer, she sells 5 tins for GH₵ 66.00. By what percentage did she reduce her original price?
15 %
6 %
9 %
12 %
19.
The graph of y = x2 + 4x - 6 is drawn and a linear graph is drawn on the axes such that the intersection of the two graphs gives the solution to the equation x2 + 4x - 7 = 0. Find the equation for the linear graph.
x = 1
x = -1
y = 1
y = 1
20.
The interior angle of a regular polygon is twice the exterior angle. How many sides has the polygon?
5
6
8
9
21.
Metuh is nine times as old as his cousin, Fafa. In six years time, he will be five times as old as Fafa. Find Fafa's present age.
5 years
6 years
7 hears
8 years
22.
If A = b(a + b), make a the subject of the relation.
a = b -
a = - b
a = + b
a = - b
23.
Evaluate
6.65 x 108
6.65 x 107
6.65 x 10-7
6.65 x 10-8
24.
If = , find x:y
5:3
4:1
3:5
1:4
25.
Find the equation of the line passing through P(4,1) and parallel to 2x + 5y = -10.
5x + 2y = 13
5x - 2y = 10
2x - 5y = 10
2x + 5y = 13
26.
The exterior angles of a quadrilateral are 61°,76°, (x + 10)° and (2x + 45)°.
Find the value of x.
45
60
66
56
27.
If 17 = 3 mod x, find the least value of x.
3
5
7
9
28.
The shadow of a vertical pole is 50 cm. If the height of the pole is 2 m, find, correct to the nearest degree, the angle of elevation of the sun from the ground level.
45°
56°
60°
76°
29.
Consider the following statements:
M: Helena studies hard;
N: Helena passes her examination.
If M ⇒ N
If Helena does not study hard, then she will pass her examination.
If Helena does not study hard, then she will not pass her examination.
If Helena passes her examination, then she had not studied hard.
If Helena does not pass her examination, then she had not studied hard.
30.
The area of a sector of a circle is 40 cm2. If the sector subtends an angle of 140° at the centre, find the area of the circle.
102.86 cm2
111.56 cm2
120.38 cm2
132.06 cm2
31.
Given that 6log(x + 4) = log64, find the value of x.
4
2
-2
-4
32.
A die is rolled once. Find the probability of obtaining a number less than 3.
33.
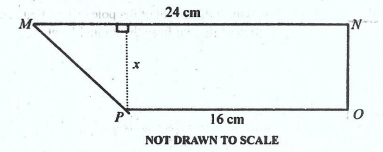
If the area of the trapezium MNOP is 300 cm2, find the value of x.
15 cm
12 cm
10 cm
20 cm
34.
Find the 11th term of , ,1, 1, ... .
8
6
4
2
35.
In a class of 30 students, 18 takes Mathematics, 5 take both Mathematics and Biology and 8 take neither Mathematics nor Biology. Find the number of students that take Biology.
6
8
9
13
36.
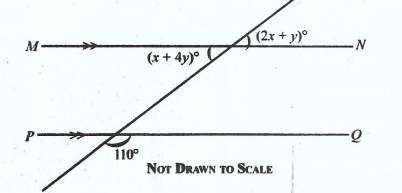
In the diagram, MN // PQ. Find the value of (x + y).
90°
60°
40°
30°
37.
Simplify .
5
3
38.
The length of a rectangular lawn is 3 cm longer than the width. If the perimeter is 42 cm, find the width.
6 cm
9 cm
12 cm
15 cm
39.
Given that p = x - and q = x2 + , express q in terms of p.
q = (p2 + 2)
q = (p - 2)2
q = (p + 2)2
q = (p2 - 2)
40.
A car moves at an average speed of 30 kmh-1. How long does it take to cover 200 metres?
2.4 seconds
24 seconds
144 seconds
240 seconds
41.
If y varies as the square of x, y = 3 when x = , find the value of y when x = 2
2
4
5
6
42.
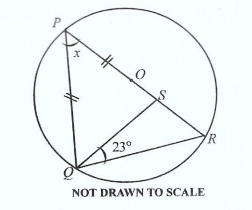
In the diagram, O is the centre of the circle PQR, |PS| = |PQ| and ∠RQS = 23o. Find the value of x.
23o
38o
46o
67o
43.
The mass of some market women in kg are: 83, 47, 62, 49, 55, 72, 58 and 62.
Use the information to answer the question below
Find the range.
21
36
46
52
44.
The mass of some market women in kg are: 83, 47, 62, 49, 55, 72, 58 and 62.
Use the information to answer the question below
Find the mean.
45
55
61
71
45.
Evaluate tan 30o - 2sin 60o
- 1
46.
Simplify: 8 - .
3
3
3
3
47.
The probabilities of three independent events X, Y and Z occurring are , and respectively. What is the probability that only events X and Z are occurring?
48.
One side of a rectangle is 8 cm and the diagonal is 10 cm. Calculate the area of the rectangle.
60 cm2
48 cm2
40 cm2
24 cm2
49.
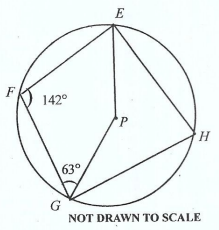
In the diagram, EFGH are points on a circle centre P. If ∠ EFG = 142o and ∠ FGP = 63o, find ∠ FEP.
63o
76o
79o
89o
50.
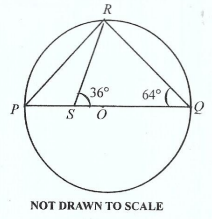
In the diagram PQ is the diameter of circle PQR with centre O and RS meets PQ at S.
If ∠ RQP = 64o and ∠ RSQ = 36o, find ∠ PRS.
22o
18o
16o
10o
The third and eighth terms of a Geometric Progression (G.P) are 4 and respectively. Find the:
(a)
common ratio;
(b)
first term;
(c)
sum of the first and second terms.
In a school election for the position of SRC President, one candidate obtained 87.5% of the votes cast. The other candidates obtained a total of 275 votes.
(a)
How many votes did the winner obtained.
(b)
If the voter turnout was 55%, find the total number of eligible voters in the school.
A mason hired a labourer to fill a cubic rubber tank of length 1.2 m with water.
The labourer used a container of volume 54 litres. If the mason agreed to pay GH₵ 1.75 for a container of water fetched, calculate:
(a)
in litres, the volume of the tank;
(b)
the number of containers of water that can fill the tank;
(c)
the amount of money paid to the labourer to fill the tank with water.
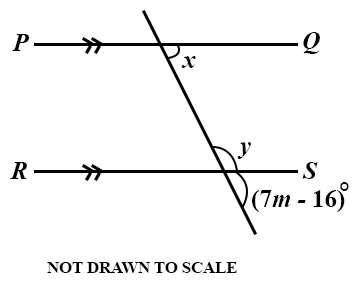
In the diagram PQ//RS. Given that x : y = 2 : 7, find the value of m.
(a)
Given that sin y = , 0° ≤ 90°, evaluate .
(b)
A number is chosen at random from the set of integers, 10 to 30 inclusive.
Find the probability that the number is a multiple of 3 or 4.
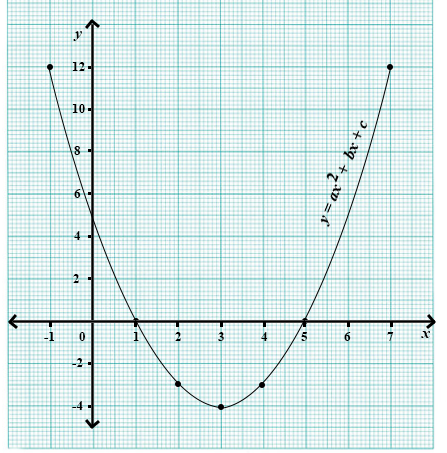
The graph shows the relation of the form y = ax2 + bx + c, where a, b and c are constants.
(a)
State the scale used for each axes.
(b)
Find the values of a, b and c.
(c)
Find the values of x when y = 7.
(d)
Write the coordinates of the minimum point.
(e)
State the range of values of x for which y < 0.
The estimated cost of building a two bedroom house is GH₵ 120,000.00. It is made up of labour, materials and consultancy fee in the ratio 5 : 12 : 3 respectively. At the start of the construction, the labour cost increased by 2y %, cost of materials increased by 2.5y% while consultancy fee remain unchanged. If the new cost of labour is two-fifth the new cost of materials, find the:
(a)
value of y;
(b)
new cost of building the house.
(a)
Kojo can do a piece of work in 5 hours. Edna can do the same piece of work in 4 hours. How long will it take the two of them to do the same work together, if they worked at the same rate?
(b)
A solid right triangular prism of length 12 cm and a cross-section which is an equilateral triangle of side 6 cm. Find, correct to four significant figures, the total surface area.
(a)
Copy and complete the table of values for y = cos x - 3 sin x, 0° ≤ x ≤ 180°.
| x | 0° | 20° | 40° | 60° | 80° | 100° | 120° | 140° | 160° | 180° |
| y | 1.0 | -2.1 | -2.0 |
(b)
Using a scale of 2 cm to 20° on the x axis and 4 cm to 1 unit on the y axis, draw the graph of y = cos x - 3 sin x, 0° ≤ x ≤ 180°.
(c)
Using the graph, find the:
(i)
truth set of 2 + cos x = 3 sin x;
(ii)
range of values of x for which y increases as x increases;
(iii)
minimum point of the curve.
| Age (years) | 7 | 8 | 9 | 10 | 11 | 12 |
| Number of children | 2x | 3x | 4x - 1 | x | x - 2 | x - 3 |
The table shows the ages in years of 42 children at a birthday party.
(a)
Find the value of x
(b)
Calculate, correct to the nearest whole number, the mean age.
(c)
Find the probability of selecting at random a child whose age is not less than 9 years.
(a)
Given that cos (2x + 15°) = sin (x - 30°), 0° ≤ x ≤ 90°, find the value of x.
(b)
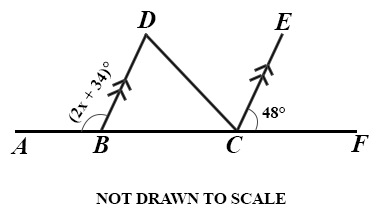
In the diagram, ABCF is a straight line, BD//CE, ∠ ABD = (2x + 34)°. If ∠ BCD = ∠ BDC and ∠ FCE = 48°, find:
(i)
the value of x;
(ii)
∠ BDC.
(a)
Fifteen persons were shortlisted for a job interview. On the day of the interview, each applicant was assigned a number from 1 to 15. An applicant was called at random from the list of numbers. Find the probability that the applicant called has the number which is:
(i)
prime;
(ii)
multiple of 3;
(iii)
divisible by 5.
(b)
PQRS is a quadrilateral with P(4, 4), S(8, 8) and R(12, 8).
If PQ→ = 4SR→, find the coordinates of Q.
(a)
The hour hand of a 24 hour clock moves from 13:15 p.m. to 17:45 p.m.
If the length of the hour hand is 3.5 cm, find correct to three significant figures, the area swept by the hour hand.
[Take π = ]
(b)
The coordinates of two points M and N in a plane are (-4, 3) and (x, 6) respectively.
If |MN| = 3 units, find the value of x.