1.
A point on the ground is 5 m away from the foot of a vertical wall 12 m high.
Calculate, correct to the nearest degree, the angle of depression of the point from the top of the wall.
25o
23o
67o
65o
2.
The gradient of the line passing through the points (3, 6) and (x, 4) is - . Find the value of x.
3
8
6
5
3.
A woman pours 85 litres of kerosene into a cylindrical container with radius 7 cm.
Calculate, correct to the nearest cm, the depth of the kerosene in the container.
[Take π = ]
240 cm
552 cm
480 cm
595 cm
4.
Given that x2 - 11x + m is a perfect square, find the value of m.
121
5.
The sides of a scalene triangle are 4 cm, 9 cm and 11 cm. Calculate, correct to the nearest whole number, the area of the triangle.
13 cm2
17 cm2
21 cm2
19 cm2
6.
In a hall, there are 175 persons. 12% are children, 56 are men and the rest are women. If one person is selected at random from the hall, find the probability that a woman is selected.
7.
A student measured the length of a classroom and obtained 3.99 m which is less than the actual length. If the percentage error was 5%, what was the actual length?
3.80 m
3.78 m
4.18 m
4.20 m
8.
A car covers the first 80 km of a journey in 2 hours and completes the journey by travelling further 2.5 hours at 50 km/h. What is the average speed of the entire journey?
44 km/h
45 km/h
47 km/h
63 km/h
9.
If log x = 2 - 3log 2, find the value of x.
10.
The graph of y = x2 - 5x + k passes through the point (3, 1). Find the value of k.
2
3
7
5
11.
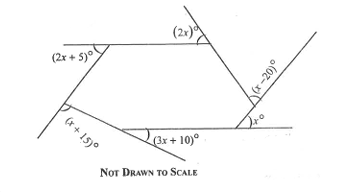
Find the value of x in the diagram.
41
37
35
31
12.
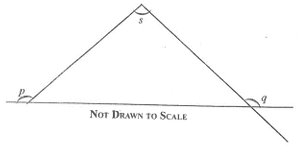
In the diagram, p + q = 250o. Find the angle marked s.
70o
110o
290o
250o
13.
If x : y : z = 2 : 3 : 4, evaluate .
1.5
2.5
2.0
3.0
14.
Find the mean of (x + y), (2x + 3y), (2x - 2y) and (3x - 2y).
4x
x
2x
3x
15.
A box contains 2 red, 6 white and 5 black balls, all of the same size. If a ball is selected at random, what is the probability that it is black?
16.
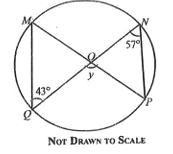
In the diagram, MNPQ is a circle, centre O. ∠ MQN = 43o and ∠ QNP = 57o.
Find the value of y.
70o
90o
80o
100o
17.
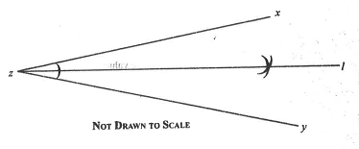
Describe the locus, l in the diagram.
Locus of points equidistant from x and z.
Locus of points equidistant from x and y.
Locus of points equidistant from xy and zy.
Locus of points equidistant from zx and zy.
18.
The base radius and slant height of a solid cone are 8 cm and 14 cm respectively. Calculate, correct to two decimal places, its volume.
[Take π = ]
553.14 cm3
640.87 cm3
838.67 cm3
770.32 cm3
19.
Abudu can do a piece of work in 6 days and Efah can do the same work in 3 days. What fraction of the work can both do together in a day?
20.
If P = {x: 1 ≤ x ≤ 6} and Q = {x: 2 < x < 9} where x ∈ R, find P ∩ Q.
{x: 2 ≤ x < 6}
{x: 2 ≤ x ≤ 6}
{x: 2 < x ≤ 6}
{x: 2 < x < 6}
21.
Given that p2 + q2 + r2 = 50, p = 5 and = 2, find the positive value of r.
5
3
4
2
22.
If and -3 are the roots of px2 + qx + r = 0, find the values of p, q and r.
p = 2, q = -5, r = 3
p = 2, q = 5, r = 3
p = 2, q = 5, r = -3
p = -2, q = 5, r = 3
23.
A cylindrical container closed at both ends has radius 5 cm and height 10 cm. Calculate to two decimal places, the total surface area.
[Take π = ]
470.43 cm3
471.43 cm3
456.43 cm3
460.43 cm3
24.
Badu is four times as old as Juliet. In 10 years Badu will be twice as old as Juliet. Find Juliet's age.
3 years
6 years
5 years
8 years
25.
When the point (4, 5) is rotated through an angle in the anticlockwise direction about the origin, its image is (-5, 4). What is the angle of rotation?
90o
270o
180o
300o
26.
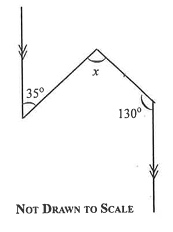
Find the value of x in the diagram.
165o
50o
95o
85o
27.
A woman bought a washing machine for $18,000.00. If the exchange rate is $0.045 to ₦1.00, find in ₦, the cost of the machine.
₦ 400,000.00
₦ 600,000.00
₦ 250,000.00
₦ 300,000.00
28.
Determine the least value of x such that 7 + x = 3 (mod 8).
3
4
5
6
29.
If = , find the ratio of m : n.
4 : 7
4 : 3
3 : 4
7 : 4
30.
Yakubu received 12% of the sales made in a certain mouth. If the amount he received was $35,000.00, what was the total sales made?
$245,000.00
$140,000.00
$315,000.00
$280,000.00
31.
The angle of elevation of the top of a vertical pole from a point, P on a level ground is 60°. The distance from P to the foot of the pole is 55 m. Find the height of the pole.
m
55 m
m
m
32.
The ratio of girls to boys in a certain committee is 5 : 2. If there are 35 members in the committee, how many more boys must be added to the committee to have the ratio of girls to boys as 5 : 4?
20
10
15
5
33.
Find the values of x for which is not defined.
x = 2, -4
x = 4, -4
x = -2, 2
x = 0, 2
34.
Given that tan x = , find the value of (sin x cos x)
35.
Consider these two statements:
P: N is an odd number
Q: N is a prime number greater than 2.
Express "If N is not an odd number then N is not a prime number greater than 2" in symbolic form.
~P ⇒ Q
~P ^ ~Q
P ⇒ ~Q
~P ⇒ ~Q
36.
A sector which subtends an angle 150° is cut from a circular plate of radius 14 cm.
Find, correct to one decimal place, the perimeter of the remaining plate.
[Take π = ]
65.3 cm
79.3 cm
84.7 cm
64.7 cm
37.
One side of a gutter is 15 cm lower than the other side. A plank of wood, which is laid across the gutter to form a bridge, slopes at an angle of 35° to the horizontal. How wide is the gutter?
18.31 cm
21.42 cm
26.15 cm
10.50 cm
38.

In the diagram, MOP is the diameter of the circle MNP centre O. ∠ NMP = (2x)° and ∠ EPM = (5x + 18)°. Find the value of x.
72°
24°
48°
18°
39.
The height of a square base pyramid is thrice the length of a side of its base. If the base area is 324 cm2, find the volume of the pyramid.
17,496 cm3
5,832 cm3
324 cm3
972
40.
If 4x = , find the value of x
-10
-5
8
4
41.
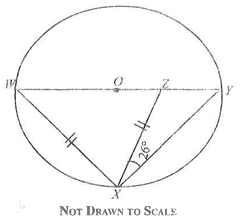
In the diagram, O is the centre of the circle WXY. |WX| = |XZ| and ∠ ZXY = 26°. Find ∠ XYZ.
62°
42°
52°
32°
42.
Evaluate 141six + 233six - 102six
412six
405six
312six
305six
43.
In the first year, Mr. Kwakye's annual salary was $1,560.00. His salary was increased each year by a constant value, y until it was $13,980.00 in the 13th year. Calculate the value of y.
$955.38
$1,230.00
$1,129.09
$1,035.00
44.
Given that , x, 1, y is a Geometric Progression (G.P), find the value of xy.
2
1
45.
A chord of a circle, 12 cm long subtends an angle of 150° at the centre of the circle. Find the radius of the circle.
3.0 cm
4.3 cm
6.0 cm
6.2 cm
46.
The lines 3x + 2y = 4 and y = 2x - 5 intersect at a point P(x, y). Find the coordinates of P.
(2, 1)
(-2, 1)
(2, -1)
(-2, -1)
47.
Make u the subject of the relation = .
u = s - t
u = t - s
u = ts
u = t + s
48.
| Number of subjects | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of students | 2 | 1 | 4 | 3 | 8 | 5 | 4 | 3 |
The table shows the number of subjects registered by a class of students for an examination.
Use the information to answer the question below
Calculate the mean of the distribution.
2
3
8
5
49.
| Number of subjects | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of students | 2 | 1 | 4 | 3 | 8 | 5 | 4 | 3 |
The table shows the number of subjects registered by a class of students for an examination.
Use the information to answer the question below
Find the median.
2
5
3
8
50.
A rectangular tank of sides 4 m by 8 m by 11 m has the same volume as a cylindrical tank of height 7 m.
Calculate the base radius of the cylindrical tank.
[Take π = ]
4 m
22 m
8 m
88 m
In a talent hunt competition of 35 artists, they indicated their interest in playing Cymbal, Saxophone and Bongo. Out of the number, 24 preferred Cymbal, 15 Saxophone and 18 Bongo. 8 preferred Cymbal only, 2 Saxophone only and 6 Bongo only. 4 played all the three instruments while 7 preferred Cymbal and Saxophone only.
(a)
Illustrate the information in a Venn diagram.
(b)
Find the number of artists who preferred:
(i)
only two types of instruments;
(ii)
only one type of instrument.
Doris walked 2t km from a village, K to visit a friend in another village, L on a bearing of 065°. After spending some time with her friend, she continued to a nearby town, M 3t km away on a bearing 155°. If the distance between K and M is 6 km:
(a)
illustrate the information in a diagram;
(b)
calculate, correct to the nearest whole number, the:
(i)
value of t;
(ii)
bearing of M from K.
In the frustum of a cone, the bottom diameter is thrice the top diameter.
(a)
If the height of the frustum is 12 cm, calculate the height of the whole cone.
(b)
Given that the volume of the whole cone is 39,600 cm3, find, correct to four significant figures, the radius.
[Take π = ]
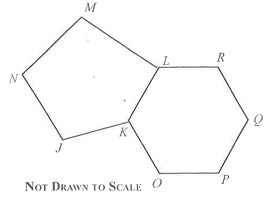
In the diagram, JKLMN is a regular pentagon and KOPQRL is a regular hexagon. Find:
(a)
∠ JNM;
(b)
∠ KOP;
(c)
∠ MLR.
The mean age of a second year class of a school is 18. At the end of the promotion examination, 3 students aged 20, 19 and 19 years were repeated. The new mean age of the class became 18.
Calculate the number of students who were in the class before the promotion examination.
(a)
In a certain spider web, the lengths of the shortest and longest threads are 3.4 mm and 50.2 mm respectively. The successive equally spaced threads are 1.2 mm apart.
If the length of the cross threads form an Arithmetic Progression (A.P), find the number of cross threads.
(b)
At noon, a cargo plane leaves Moi airport and heads towards Kisumu 500 km away at 180 km/h. At 1.00 pm, a jet takes off from Moi and flies on the same course at 450 km/h.
What time will the jet overtake the cargo plane?
A man left an estate for his wife, extended family and children, Dakorah, Gifty and Gemma.
In the will, of the estate must be given to Dakorah, of the remaining to Gifty, of what still remains to Gemma, of the remaining to the wife and the rest to the extended family.
If the wife received a total of GH₵ 105,500.00 as her share of the estate, find the
(a)
total value of the estate
(b)
extended family's share of the estate.
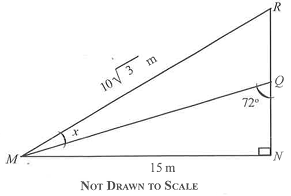
In the diagram, MNR is right angle triangle. |MN| = 15 m, |MR| = 10 m and ∠ MQN = 72°.
Calculate, correct to the nearest whole number:
(a)
the value of the angle marked x;
(b)
|QR|;
(c)
area of ∆ MQR.
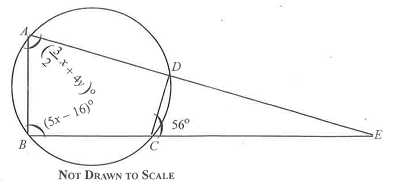
In the diagram, A, B, C, D are points on a circle. ADE and BCE are straight lines.
∠ DCE = 56°, ∠ ABE = (5x - 16)° and ∠ BAE = °. If ∠ DCE : ∠ CDE = 7:8;
find:
(a)
∠ AEB;
(b)
the values of x and y.
(a)
A cupboard contains three kinds of notebooks: J, K and L, all of the same size.
The number of book J is 3 more than half of book L. The number of K is one-third the number of L.
(i)
If there are 25 books in the cupboard, find the number of each kind of book.
(ii)
If a book is picked at random from the cupboard, what is the probability that it is K or L?
(b)
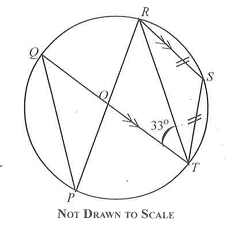
In the diagram PQRST is a circle with centre O. POR and QOT are straight lines, QT||RS, ∠ RTQ = 33° and |RS| = |ST|.
Find ∠ RST.
(a)
From the top, X of a building 320 m high, the angles of depression of the top, Y and bottom, Z of another building on the same horizontal ground are 29° and 41° respectively.
(i)
Illustrate the information in a diagram.
(ii)
Calculate, correct to the nearest metre, the height of the other building.
(b)
The time taken to travel a distance of 120 km was reduced by 30 minutes when the speed was increased by 20 km/h. Calculate the initial speed.
(a)
The following statements are true of a certain community.
S: Most businessmen are rich.
T: No salary worker is rich.
(i)
Draw a Venn diagram to illustrate the information.
(ii)
State whether the following statements are Valid or Not Valid.
(α)
Ali is a businessman and therefore rich.
(β)
Ahmed is not rich because he is a salary worker.
(b)
| Heights(cm) | 60 - 64 | 65 - 69 | 70 - 74 | 75 - 79 | 80 - 84 |
| Frequency | 7 | 6 | 5 | 8 | 4 |
The table shows the distribution of height of seedlings in a nursery. Calculate, correct to one decimal place, the:
(i)
mean;
(ii)
variance of the distribution.
(a)
Using a scale of 2 cm to 1 unit on both axes, draw on a graph sheet two perpendicular axes ox and oy for 0 ≤ x ≤ 8 and -6 ≤ y ≤ 6.
(i)
Plot the points M(3,1), N(1,1) and P(3,5). Join the points to get △MNP.
(ii)
Draw image triangle M1N1P1 which is the reflection of △MNP in the x - axis where M → M1, N → N1 and P → P1. Indicate clearly the coordinates of M1, N1 and P1.
(iii)
Draw the image triangle M2N2P2 which is the image of △MNP under the mapping → , where M → M2, N → N2 and P → P2. Indicate clearly the coordinates of M2, N2 and P2.
(b)
Find the equation of the line joining the points M and M2.