1.
The sum of the interior angles of a polygon is 1260°. Find the number of sides.
9
6
7
8
2.
A building is 12 m high. A football on the ground floor s 30 m away from the foot of the building.
Find, correct to the nearest degree, the angle of depression of the ball from the top of the building.
22°
68°
66°
24°
3.
A number is chosen at random from the set {13, 14, ...., 30}. What is the probability that it is a prime number?
4.
Regina is 34 years old and her daughter is 5 years. In n years, Regina will be twice as old as her daughter. Find the value of n.
23
30
29
24
5.
If P(-7, 8) is reflected in the line x - 2 = 0, find the coordinates of the image of P.
6.
If the variable P is inversely proportional to Q2 and P = 2.25 when Q = 6, find P when Q = 3.
9.5
7.5
8.5
9.0
7.
Make x the subject of the relation y = .
x =
x =
x =
x =
8.
Seven men complete a certain work schedule in 6 days. How long will it take two of the men to complete the same work schedule f they work at the same rate?
42 days
35 days
21 days
14 days
9.
If cos y is negative and sin y is negative, in which quadrant would y lie?
First
Fourth
Third
Second
10.
The volume of a cone s 264 cm3. If the base radius is 6 cm, find the height.
[Take π = ]
5 cm
8 cm
7 cm
6 cm
11.
Find the value of x for which is not defined.
1
2
-1
12.
The range of a sample of 10 numbers is 5 and the largest value is 50. What is the least value?
40
60
55
45
13.
The mean of ten numbers is 16. When another number, k, is added, the mean becomes 18.
Find the value of k.
38
32
34
36
14.
The probability that John and James pass an examination are and respectively.
Find the probability that both will fail.
15.
The diagonals of a rhombus are 12 cm and 16 cm.
Find the perimeter.
42 cm
24 cm
28 cm
40 cm
16.
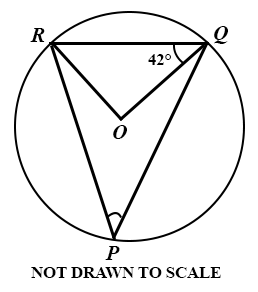
In the diagram PQR is a circle with centre O and ∠ OQR = 42°.
Find ∠ QPR.
42°
48°
54°
56°
17.
Solve: x(3x + 4) = 4.
x = or x = - 2
x = - or x = 2
x = or x = 2
x = - or x = - 2
18.
If P = {-2, 0, 2, 4, 6} and Q = {-3, -1, 0, 2, 3, 5}, find the set P ∩ Q.
{}
{-3, -1, 3, 5}
{-2, 4, 6}
{0, 2}
19.
An office equipment depreciates at 15% per annum. If the cost is GH₵ 1,200.00 when new, find the value after three years.
GH₵ 936.00
GH₵ 867.95
GH₵ 736.95
GH₵ 876.00
20.
Solve: - = .
x = 0
x = 5
x = 4
x = 2
21.
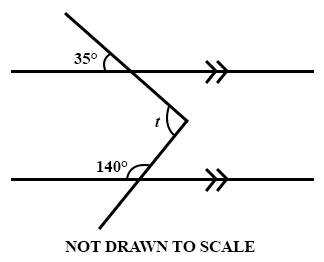
Calculate the value of t in the diagram.
35°
175°
75°
40°
22.
Given that 6 ⊗ 7 = y (modulo 8), find the value of y.
2
5
4
3
23.
Express 0.0063075 correct to three significant figures.
0.006
0.0063
0.00631
0.0060
24.
Given the statements p and q, the statement p ∨ q is false only if
p is false and q is true.
p is true and q is true.
p is false and q is false.
p is true and q is false.
25.
| y | 1 | 2 | 3 | 4 |
| x | 0 | 2 | 4 | 6 |
The table describes the relation y = mx + c where m and c are constants.
Use the information to answer the question below
What is the gradient of the equation of the line?
-2
2
1
26.
| y | 1 | 2 | 3 | 4 |
| x | 0 | 2 | 4 | 6 |
The table describes the relation y = mx + c where m and c are constants.
Use the information to answer the question below
Find the equation of the line described in the table.
y = 2x
2y = x + 2
y = x
y = x + 1
27.
The second term of a Geometric Progression (G.P) is 9. If the fourth term is 81, find the common ratio.
4
1
2
3
28.
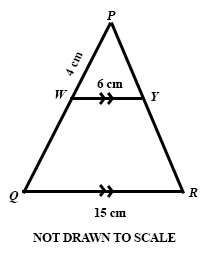
In the diagram, ∆PQR is similar to ∆PWY. WY||QR, |QR| = 15 cm, |WY| = 6 cm and |WP| = 4 cm.
Find |WQ|.
6 cm
12 cm
10 cm
8 cm
29.
A cylindrical container closed at both ends has a radius of 3 cm and height of 4 cm.
What is the total surface area of the container?
[Take π = ]
103.7 cm2
132.0 cm2
125.7 cm2
113.1 cm2
30.
The diameter of a bicycle wheel is 21 cm. If the wheel makes 8 complete revolutions, what will be the total distance covered by the wheel?
[Take π = ]
132 cm
1,386 cm
1,056 cm
528 cm
31.
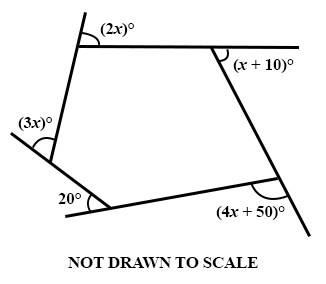
Find the value of x in the diagram.
16
44
36
28
32.
The interior angles of a triangle are (y + 10)°, (2y - 40)° and (3y - 90)°.
Which of the following accurately describes the triangle?
isosceles triangle
right-angled triangle
equilateral triangle
scalene triangle
33.
Given that sin A = , 0° ≤ A ≤ 90°, find the value of (tan A - cos A)
-
-
34.
Simplify: 3 log x + log y - 2 log z.
log (x3yz2)
log ()
log ()
log ()
35.
Simplify: .
36.
The area of a square parcel of land is 256 m2. A rectangular field of length 20 m has the same perimeter as the parcel of land.
Find the area of the field.
144 m2
400 m2
320 m2
240 m2
37.
Mr. Abban invested $1,200.00 for 3 years at 5% per annum compound interest.
Find the interest earned at the end of three years.
$189.15
$1,389.15
$1,380.00
$180.00
38.
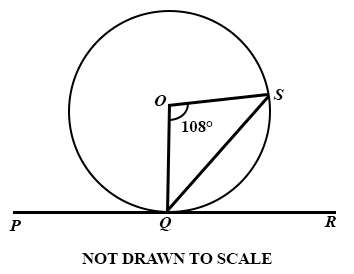
In the diagram PR is tangent to the circle at Q. The centre of the circle is O and ∠ QOS = 108°.
Use the information to answer the question below
Find ∠ OSQ.
72°
18°
36°
42°
39.

In the diagram PR is tangent to the circle at Q. The centre of the circle is O and ∠ QOS = 108°.
Use the information to answer the question below
Find ∠ SQR.
36°
72°
54°
42°
40.
Find the value of x that satisfies the equation: (x + 5) = 1 - .
1
4
3
2
41.
A closed cuboid has length 12 cm, width 7 cm and height 5 cm. Calculate the total surface area.
179 cm2
420 cm2
358 cm2
210 cm2
42.
Mr. Amuzu sold his car through an agent who charged 9% commission on the selling price.
If Amuzu received GH₵ 236,600.00 after the sale, find the selling price of the car.
GH₵ 238,400.00
GH₵ 248,000.00
GH₵ 260,000.00
GH₵ 273,000.00
43.
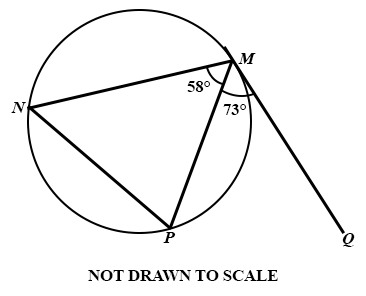
The diagram shows a triangle MNP inscribed in a circle. MQ is a tangent to the circle at M.
Find ∠ MPN.
49°
131°
73°
58°
44.
In an examination taken by 120 students, 90 passed Mathematics, 40 passed Science and 5 failed both subjects.
Use the information to answer the question below
How many students passed Science only
15
75
25
20
45.
In an examination taken by 120 students, 90 passed Mathematics, 40 passed Science and 5 failed both subjects.
Use the information to answer the question below
Find the probability that a student selected at random passed only one subject.
46.
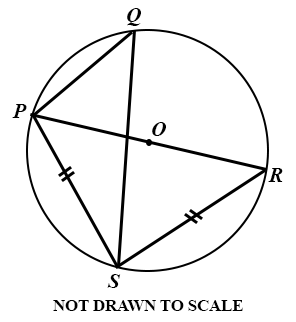
In the diagram, PR is a diameter of the circle PQS with centre O.
Find the value of ∠ PQS.
37°
90°
55°
45°
47.
If P(-7, 8) is reflected in the line x - 2 = 0, find the coordinates of the image of P.
48.
Find the product of 124seven and 23seven.
3125seven
3215seven
3211seven
3115seven
49.
Given that m = 5, n = 3 and r = 2, evaluate
1
50.
Three boys of ages 2, 4 and 10 shared 32 oranges in the ratio of their ages. What was the least share?
4
10
8
6
Monica rode a bicycle for 45 minutes and walked for an hour to cover a total distance of 10.4 km. If the riding speed is 3 times the walking speed, find, correct to two significant figures, the:
(a)
walking speed;
(b)
distance travelled by riding.
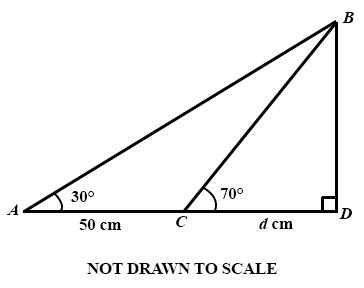
In the diagram, ABD is a triangle, |AC| = 50 cm and |CD| = d cm.
Find, correct to one decimal place,:
(a)
the value of d;
(b)
|BD|.
A man travels 4 km from a point I on a bearing of 135° to J. He continues 13 km on a bearing of 045° to K.
(a)
Illustrate the information in a diagram.
(b)
Find:
(i)
correct to two significant figures, |JK|;
(ii)
the bearing of K from I.
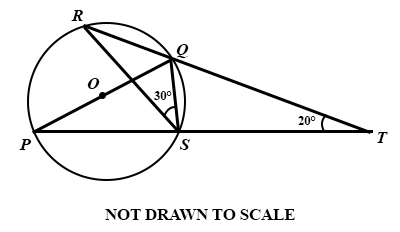
In the diagram, P, R and S are points on a circle centre O. T is a point outside the circle such that ∠ RTP = 20°, ∠ QSR = 30° and PQ is a diameter.
Calculate:
(a)
∠ QRS;
(b)
∠ PQS.
The mean age, in years, of t girls in a class was 17.6. At the end of the academic year, 4 girls aged 16, 19, 20 and 17 were dismissed. The new mean age of girls in the class became 0.2 less than the original mean.
Find the value of t.
(a)
Two towns, U and V on the equator are on longitude 67°E and 124°E respectively.
(i)
Illustrate the information in a diagram.
(ii)
Find the distance between U and V along the equator.
(iii)
How far is U from the North pole?
[Take R = 6,400 and π = ]
(b)
L(2, -1), M(3, 5), N(-1, 6) are the coordinates of the vertices of triangle LMN.
Find, correct to one decimal place, the perimeter of the triangle.
(a)
The time a man takes to paint a room alone is an hour less than the time his apprentice takes to paint the same room.
If both of them take 72 minutes to paint the room, find the time that the apprentice takes to paint the room alone.
(b)
The angle of elevation of the top of a tower from the top of a building, 5 m high is 30°. If on the horizontal ground, the building is 40 m away from the foot of the tower:
(i)
illustrate the information in a diagram.
(ii)
calculate, correct to three significant figures, the height of the tower.
(a)
A company bids for two contracts G and H. The probabilities that it will win contracts G and H are and respectively.
Find the probability that the company wins:
(i)
both contracts;
(ii)
only one contract.
(b)
Amaka drove a car from Samoa to Mepeasem at an average speed of 60 km/h in 135 minutes. On her return journey, she took 3 minutes less to arrive at Samoa.
Find correct to one decimal place the:
(i)
distance between Samoa and Mepeasem;
(ii)
the return speed.
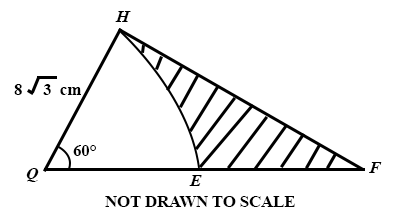
In the diagram, EH is an arc of a circle centre O. FH is a tangent to the circle at H and QF is a straight line |QH| = 8 cm and ∠ EQH = 60°.
Calculate:
(a)
the length of EF;
(b)
correct to three significant figures, the area of the shaded portion.
[Take π = ]
(a)
At a sports festival, the number of individuals who like football is thrice the number who like basketball. Those who like both games is one-third those who like basketball.
(i)
Illustrate the information in a Venn diagram.
(ii)
If 139 out of the 1,382 persons at the festival did not like any of the two games, find the number of persons who like:
(α)
football;
(β)
one type of game only.
(b)
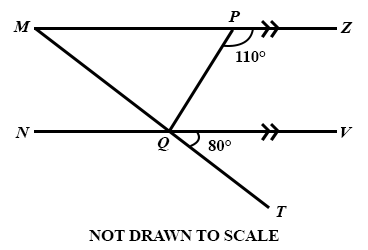
In the diagram MZ||NV. If ∠ QPZ = 110° and ∠ TQV = 80°, find ∠ PQM.
(a)
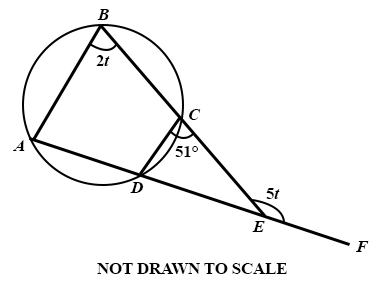
In the diagram, ABC is a cyclic quadrilateral. BC and AD are produced to E.
∠ ABC = 2t, ∠ CEF = 5t and ∠ DCE = 51°.
Find:
(i)
the value of t;
(ii)
∠ ADC
(b)
The graph of the relation y = x2 + ax + b, where a and b are constants, cuts the x axis at 3 and the y axis at 6.
(i)
Find the values of a and b.
(ii)
Use the values of a and b to solve x2 + ax + b = 0.
(a)
Abiola starts a business with $1,250.00. Frances joins the business later with a capital of $1,875.00. At the end of the first year, profits are shared equally between Abiola and Frances. When did Frances join the business?
(b)
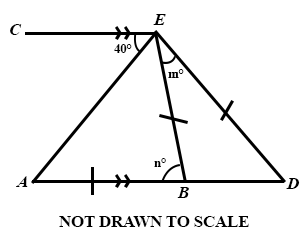
In the diagram, CE||AD and ED = EB = AB, find the value of:
(i)
n;
(ii)
m.
| Height (m) | 9 | 10 | 11 | 12 | 13 | 14 |
| Number of buildings | 5 | 4 | 6 | 5 | 6 | 4 |
The table shows the height (m) of 30 selected buildings in a town.
(a)
Find the mean height of the buildings.
(b)
Calculate, correct to one decimal place, the:
(i)
median;
(ii)
mean deviation.