1.
2.
Arrange the following in ascending order of magnitude: 0.45, and 25%
, 0.45, 25%
, 25%, 0.45
0.45, 25%,
25%, 0.45,
3.
If log102 = 0.3010 and log102y = 1.8060, find, correct to the nearest whole number, the value of y.
7
6
5
4
4.
Simplify:
2
5.
Which of the following describes the set P = {1,2,3,4,5,6}?
P = {Prime numbers < 7}
P = {x:x is a positive integer < 7}
P = {rational numbers < 7}
P = {x:x is a real number < 7}
6.
If y varies inversely as x and y = 6 when x = 3, find y when x = 9
4
3
2
1
7.
If the sequence x, 4, 16, y is Geometric Progression (GP), find the ratio of x : y.
64 : 1
8 : 1
1 : 3
1 : 64
8.
Make x the subject of the relation:
E = + z.
x =
x =
x =
x =
9.
If =
42
45
54
64
10.
Find the equation whose roots are - and 1.
2x2 -4x + 6 = 0
4x2 -4x - 3 = 0
2x2 +3x + 4 = 0
4x2 -4x + 3 = 0
11.
The graph is for the relation: y = d - x.
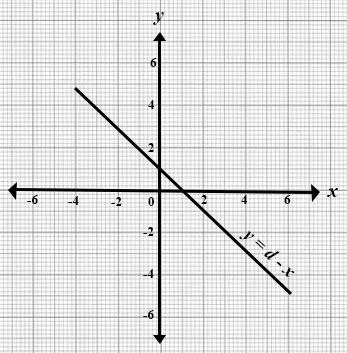
Find the value of d.
2
1
0
-1
12.
Factorize: p2q2 - 6pqr + 9r2
(pq - 3r)2
(pq - 3r)(pq + 3r)
(pq + 3r)2
(pr + 3q)(pr - 3q)
13.
An empty rectangular tank is 250 cm long and 120 cm wide. If 180 litres of water is poured into the tank, calculate the height of the water.
4.5 cm
5.0 cm
5.5 cm
6.0 cm
14.
The area of a trapezium is 49 cm2. If the parallel sides are 6 cm and 7 cm long, find, correct to one decimal place, the distance between the parallel sides.
6.5 cm
6.8 cm
7.4 cm
7.5 cm
15.
The area of a sector of a circle and the length of its arc are 231 cm2 and 66 cm respectively. Calculate the radius of the circle
[Take π = ]
3.5 cm
7.0 cm
10.5 cm
14.0 cm
16.
A ladder, 10 m long, touches a side of a building at a height of 8 m. At what height would a ladder with length 12 m touch the building, if it makes the same angle with the ground?
(Assume that the ladder and building are on the same horizontal ground)
10.6 m
10.4 m
10.0 m
9.6 m
17.
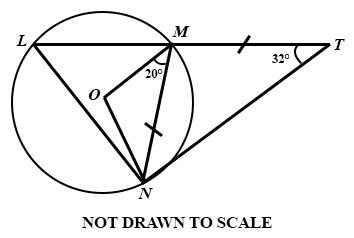
In the diagram, LMT is a straight lne. If O is the centre of circle LMN, ∠ OMN = 20°, ∠ LTN = 32° and |NM| = |MT|, find ∠ LNM.
44°
46°
52°
76°
18.
Which of these statements about an acute-angled triangle is true?
It has three equal angles.
It has two equal sides.
It has all its angles less than 90°.
It has one angle less than 90°.
19.
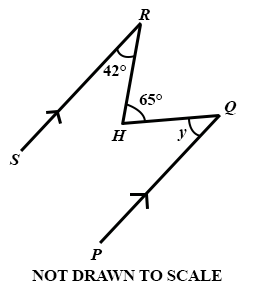
In the diagram, SR//PQ, ∠ SRH = 42°, ∠ RHQ = 65° and ∠ HQP = y. Find the value of y.
73°
65°
42°
23°
20.
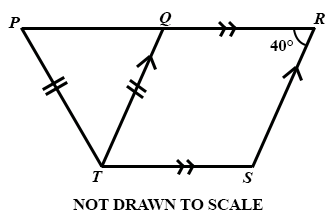
Find the value of ∠ RPT in the diagram.
20°
40°
50°
60°
21.
The points O(0, 0), P(4, -1) and Q(1, -4) are the vertices of ∆OPQ.
What kind of triangle is ∆OPQ?
Equilateral
Isosceles
Right-angled
Scalene
22.
Which of the following points lies on the graph of y = x2 + 1?
(3, 9)
(2, 8)
(3, 8)
(2, 9)
23.
A tree 8 m tall casts a shadow 10 m long.
How tall is a tree on the same ground level that casts a shadow 40 m long at the same time of the day?
32 m
50 m
80 m
96 m
24.
If cos(3x + 28°) = sin (2x + 48°), 0° ≤ x ≤ 90°, find the value of x.
2.8°
15.2°
20.0°
22.0°
25.
Sammy moved 6 km due west and then 6 km on a bearing of 300°. What is the bearing of his initial position from his final position?
105°
150°
165°
195°
26.
The table shows the distribution of the number of goals scored by a football team during a football competition.
| No. of goals | 1 | 2 | 3 | 4 | 5 |
| Frequency | 6 | 3 | 4 | 1 | 2 |
Calculate, correct to one decimal place, the mean number of the goals scored.
2.3
2.4
2.5
2.6
27.
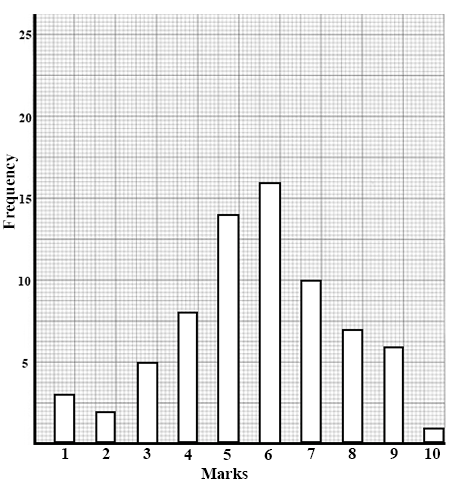
The bar chart represents the distribution of marks scored by students in a Mathematics test.
Use the chart to answer the question below
How many students took the test?
80
72
60
52
28.

The bar chart represents the distribution of marks scored by students in a Mathematics test.
Use the chart to answer the question below
If the pass mark was 5, what percentage of the students failed the test?
25%
28%
35%
42%
29.

The bar chart represents the distribution of marks scored by students in a Mathematics test.
Use the chart to answer the question below
Find the probability that a student selected at random obtained the median mark.
30.
Out of 20 girls in a class, 12 like Music and 15 like movies. If a girl is selected at random from the class, what is the probability that she liked both Music and Movies?
31.
The mean of the numbers 2, 5, 2x and 7 is not greater than 5. Find the range of values of x.
x ≤ 3
x ≥ 3
x < 3
x > 3
32.
If 3-x = k, what is 3x?
-k
3k
k3
33.
To arrive on schedule, a ferry is to cover a distance of 40 km at 50 km/h. If the ferry delays for 18 minutes before starting the journey, at what speed must it move so as to arrive on schedule?
70 km/h
80 km/h
90 km/h
100 km/h
34.
Consider the statements:
p: the well is wide;
q: the well is clean;
r: the well is deep.
Write in symbolic form the statement "if the well is wide and clean, then it is deep".
p ∧ q → r
p ∨ q → r
p ∧ q ∨ r
p ∨ q ⇔ r
35.
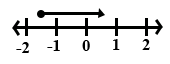
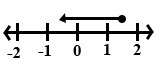
Which of the following number lines illustrates the solution of (2x - 9) ≥ 2(2x + 1)?
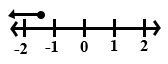
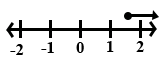
36.
10101
1001
+*****
111001
10111
11001
11011
11010
37.
A woman was y years old when she had a daughter. When the daughter was x years old, the mother was n times as old as her daughter.
Express y in terms of n and x.
y = n(x - 1)
y = x(n - 1)
y = n - x
y = x
38.

In the diagram, O is the centre of the circle QRST. ∠ QRT = 42° and ∠ PQS = 124°.
Use it to answer the question below
Find the size of ∠ RSQ.
34°
48°
56°
76°
39.

In the diagram, O is the centre of the circle QRST. ∠ QRT = 42° and ∠ PQS = 124°.
Use it to answer the question below
Find ∠ STR.
76°
56°
34°
21°
40.
Simplify: - -
41.
Given that one of the roots of the equation 2x2 + (k + 2)x + k = 0 is 2, find the value of k
-4
-2
-1
-
42.

In the diagram, YT is a straight line, |XY| = |YZ|, |XZ| = |ZT| and ∠ XYZ = 52°.
Calculate ∠ZTX.
24°
32°
40°
64°
43.
A farmer cleared 40% of a piece of land the first day and 60% of the remainder the next day. What percentage of the land was remaining at the end of the second day?
30%
24%
20%
15%
44.
The length of an arc of a circle is 11 cm. If it subtends an angle of 60° at the centre of the circle, calculate the radius of the circle.
[Take π = ]
7 cm
7 cm
10 cm
10 cm
45.
The mean of the sum of the squared deviations from the mean is referred to as
mean deviation.
standard deviation.
variance.
actual mean.
46.
The interior angles of a pentagon are y°, 2x°, 3x°, 2x° and y°.
If y = , find the value of y.
72
81
108
126
47.
A right pyramid is on a square base, the length of the base is equal to the vertical height of the pyramid.
If the volume is 114 cm3, find its height.
4.9 cm
7.0 cm
10.1 cm
18.5 cm
48.
Given that 2x + 1 = 4(mod 7), where x is an integer.
Find the least value of x.
2
3
4
5
49.
Simplify: + .
50.
The circumference of a circular track is 9 km. A cyclist rides round it a number of times and stops after covering a distance of 302 km. How far is the cyclist from the starting point?
[Take π = ]
6 km
5 km
4 km
3 km
Solve:
(a)
(4x - 6) - (5 - 4x) ≥ 8.
(b)
the simultaneous equations:
- = ,
- = 1.
(a)
A woman spent of her monthly salary on foodstuffs, on drugs, on utility bills and had GH₵ 285.00 left. Calculate her monthly salary.
(b)
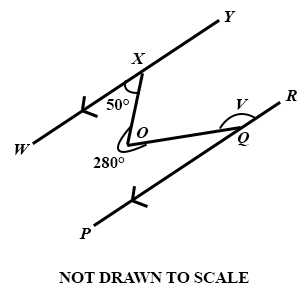
In the diagram WY // PR, ∠WXO = 50°, reflex ∠XOQ = 280° and ∠OQR = V.
Find the value of V
From two points P and Q, 15 m apart and on the same horizontal line as the foot of a tower, the angles of elevation of the top of the tower are 35° and 45° respectively.
If P and Q are on the side of the tower,
(a)
represent the information in a diagram.
(b)
find, correct to the nearest metre, the height of the tower.