FRACTIONS

A fraction is an equal part of a whole or a group.

A fraction has two parts. The number on the top of the line is called the numerator. It tells how many equal parts of the whole or collection are taken. The number below the line is called the denominator. It shows the total number of equal parts the whole is divided into or the total number of the same objects in a collection.

Fraction of a Whole

When the whole is divided into equal parts, the number of parts we take makes up a fraction.

If a cake is divided into eight equal pieces and one piece of the cake is placed on a plate, then each plate is said to have $\frac{1}{8}$ of the cake. It is read as "one-eighth" or "1 by 8"

Representing a Fraction

A fraction can be represented in 3 ways: as a fraction, as a percentage, or as a decimal.

Fractional Representation

The first and most common form of representing a fraction is $\frac{\mathrm{a}}{\mathrm{b}}$

The top (a) is known as the numerator and the down (b) is known as the denominator.

For instance in $\frac{2}{5}$, the 2 is the numerator and the 5 is the denominator

The fraction represents two parts when a whole is divided into five equal parts.

Decimal Representation

In this format, the fraction is represented as a decimal number.

The $\frac{2}{5}$, can be represented as a decimal by dividing the numerator (2) by the denominator (5).

	0.4
5	20 -20 00

$\frac{2}{5}$ = 0.4

Percentage Representation

In this representation, a fraction is multiplied by 100 to convert it into a percentage.

$\frac{2}{5}$ x 100 = 40%

We can therefore represent $\frac{2}{5}$ as 0.4 or 40%

Types of fractions

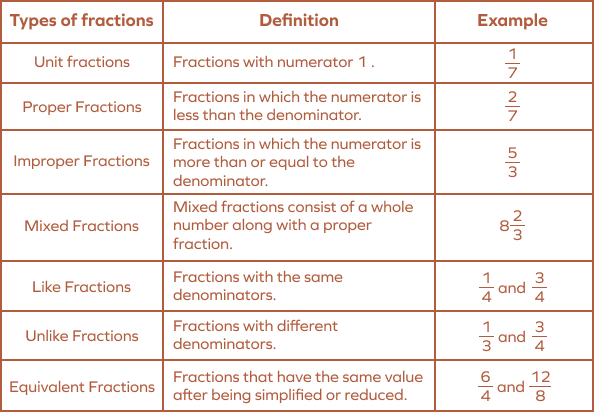
Equivalent fractions

Equivalent fractions can be obtained by multiplying both the numerator and the denominator by a non zero whole number. The new fraction is equivalent to the initial fraction.

$\frac{2}{5}$ = $\frac{\mathrm{2\; x\; 3}}{\mathrm{5\; x\; 3}}$ = $\frac{6}{15}$

$\frac{2}{5}$ and $\frac{6}{15}$ are equivalent fractions

Simplification of fractions

To express a fraction in simplest form means reducing the fraction so that the numerator and the denominator cannot be any smaller as whole numbers.

To do so, divide both the numerator and the denominator by the highest common factor.

Common means you can find at both places. Common factor(s) of two or more numbers is(are) factor(s) you can find in the list of factors of all the numbers.

As we have previously studied factors, factors of a number are the numbers that can divide exactly that number including 1 and the number itself.

Let's simplify the $\frac{6}{15}$ fraction.

Step 1

List the factors of both the numerator and the denominator

Factors of 6 = {1,2,3,6}
Factors of 15 = {1,3,5,15}

Step 2

Find the highest common factor from the list.

As you can see the highest common factor of 6 and 15 is 3

Step 3

Divide both the numerator and the denominator by the highest common factor

$\frac{6}{3}$ = 2

$\frac{15}{3}$ = 5

Hence $\frac{\mathrm{6÷3}}{\mathrm{15÷3}}$ = $\frac{2}{5}$

Hence $\frac{6}{15}$ = $\frac{2}{5}$

Changing improper fraction to mixed fraction

Improper fraction is a fraction whose numerator is larger than the denominator.

Examples

$\frac{5}{2}$ , $\frac{3}{2}$, $\frac{11}{8}$, $\frac{12}{5}$

A mixed fraction contains whole number and a proper fraction.

Improper fraction = Mixed Fraction = Whole Number Part $\frac{\mathrm{Remainder}}{\mathrm{Denominator}}$

The whole number part is the number of times the denominator can exactly divide the numerator.

The remainder is the number left after the exact division.

Examples

$\frac{5}{2}$ = 2 $\frac{1}{2}$

Explanation

2 can divide 5 exactly 2 times which is 4 (2 x 2) and 1 is left as a remainder.

To know how many times a number could exactly divide another number, you can list the multiples of the denominator to know the highest close to the number being divided.

Multiples of 2

1x 2 = 2, 2 x 2 = 4, 2 x 3 = 6,...

As you can see the closest multiple to 5 is 4 which is the multiples of 2 x 2, hence 2 can divide 5, 2 times

$\frac{3}{2}$ = 1 $\frac{1}{2}$

$\frac{11}{8}$ = 1 $\frac{3}{8}$

$\frac{12}{5}$ = 2 $\frac{2}{5}$

Converting mixed fraction to improper fraction

The general formula is:

Improper fraction = $\frac{\mathrm{Denominator\; x\; Whole\; number\; part\; +\; Remainder}}{\mathrm{Denominator}}$

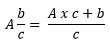
Examples

Convert the following mixed fractions into improper fractions:

7 $\frac{2}{3}$, 4 $\frac{5}{6}$, 2 $\frac{3}{8}$, 2 $\frac{3}{4}$

Solution

7 $\frac{2}{3}$ = $\frac{\mathrm{7\; x\; 3\; +\; 2}}{3}$ = $\frac{\mathrm{21\; +\; 2}}{3}$ = $\frac{23}{3}$

4 $\frac{5}{6}$ = $\frac{\mathrm{4\; x\; 6\; +\; 5}}{6}$ = $\frac{\mathrm{24\; +\; 5}}{6}$ = $\frac{29}{6}$

2 $\frac{3}{8}$ = $\frac{\mathrm{2\; x\; 8\; +\; 3}}{8}$ = $\frac{\mathrm{16\; +\; 3}}{8}$ = $\frac{19}{8}$

2 $\frac{3}{4}$ = $\frac{\mathrm{2\; x\; 4\; +\; 3}}{4}$ = $\frac{\mathrm{8\; +\; 3}}{4}$ = $\frac{11}{4}$

Ordering fractions

Key Points

It can be useful to order a group of numbers by their value. Fractions can be arranged in ascending or descending order.

Ascending: means from the smallest to the largest.

Descending: means from the largest to the smallest.

When fractions have the same denominator, the numerators are compared. The greater the numerator, the greater the fraction.

When fractions have the same numerators, the denominators are compared. The greater the denominator, the smaller the fraction.

When fractions have different numerators and denominators, they are rewritten as equivalent fractions with common denominators. The denominators then match. The numerators are compared to order the fractions.

Ordering fractions with the same denominator

When fractions have the same denominators, they are ordered by the size of their numerators:

The fraction with the smallest numerator is the smallest fraction.

The fraction with the greatest numerator is the greatest fraction.

Fractions can be arranged in ascending or descending order. Ascending order starts with the smallest value and ascends to the greatest value. Descending order starts with the greatest value and descends to the smallest value.

Two fractions can be compared in size using inequality signs (< or >)

Examples

Arrange the following fractions in ascending order

$\frac{5}{8}$,$\frac{1}{8}$,$\frac{7}{8}$,$\frac{3}{8}$

Solution

$\frac{1}{8}$,$\frac{3}{8}$,$\frac{5}{8}$,$\frac{7}{8}$

Explanation

Each fraction has the same denominator. Use the numerators to order the fractions. The smaller the numerator, the smaller the fraction.

Ordering fractions with the same numerators

To order fractions with the same numerators, the fractions are ordered by the size of their denominators.

The fraction with the smallest denominator is the greatest fraction.

The fraction with the greatest denominator is the smallest fraction.

A unit fraction has a numerator of 1. Unit fractions are also ordered using their denominators.

Examples

Arrange the following fractions in descending order.

$\frac{5}{8}$,$\frac{5}{11}$,$\frac{5}{6}$,$\frac{5}{7}$

Solution

$\frac{5}{6}$,$\frac{5}{7}$,$\frac{5}{8}$,$\frac{5}{11}$

Use the denominators to order the fractions. The smaller the denominator, the greater the fraction.

Ordering fractions with different denominators and numerators

To order fractions with different denominators and numerators, the denominators have to be the same. To do this:

Step 1

Find the least common multiple of the denominators. This will be the denominator of the equivalent fractions.

Step 2

Create the equivalent fractions by multiplying the numerator and denominator by the factor of the denominator which gives the least common multiple. The equivalent fractions should have the same denominators.

Step 3

Compare the equivalent fractions using their numerators. The greater the numerator, the greater the fraction.

Step 4

Replace the equivalent fractions by their corresponding fraction after the ordering.

Example

Arrange the fractions from smallest to greatest.

$\frac{1}{2}$,$\frac{4}{9}$,$\frac{2}{3}$

Solution

The denominators are 2,9,3

Step 1

Find the least common multiple

Multiples of 2 = {2 x 1 = 2,2x2 = 4,2 x 3 = 6,2 x 4 = 8,2x 5 = 10,2 x 6 = 12,2 x 7 = 14,2 x 8 = 16,2 x 9 = 18,2 x 10 = 20,2 x 11 = 22,...}
Multiples of 9 = {9 x 1 = 9,9 x 2 = 18,9 x 3 = 27,9 x 4 = 36,9 x 5 = 45,...}
Multiples of 3 = {3 x 1 = 3,3 x 2 = 6,3 x 3 = 9,3 x 4 = 12,3 x 5 = 15,3 x 6 = 18,3 x 7 = 21,...}

The least common multiple is 18, hence we have to find the equivalent fraction with the denominator of 18 for each of the fractions.

Step 2

Create the equivalent fractions by multiplying the numerator and denominator by the factor of the denominator which gives the least common multiple. The equivalent fractions should have the same denominators.

For the denominator 2, 2 x 9 = 18, hence we multiply both the numerator and the denominator by 9

For the denominator 9, 9 x 2 = 18, hence we multiply both the numerator and the denominator by 2

For the denominator 3, 3 x 6 = 18, hence we multiply both the numerator and the denominator by 6

$\frac{1}{2}$ = $\frac{\mathrm{1\; x\; <b>9</b>}}{\mathrm{2\; x\; <b>9</b>}}$ = $\frac{9}{\mathrm{<b>18</b>}}$

$\frac{4}{9}$ = $\frac{\mathrm{4\; x\; <b>2</b>}}{\mathrm{9\; x\; <b>2</b>}}$ = $\frac{8}{\mathrm{<b>18</b>}}$

$\frac{2}{3}$ = $\frac{\mathrm{2\; x\; <b>6</b>}}{\mathrm{3\; x\; <b>6</b>}}$ = $\frac{12}{\mathrm{<b>18</b>}}$

Step 3

Compare the equivalent fractions using their numerators. The greater the numerator, the greater the fraction.

From smallest to greatest

$\frac{8}{\mathrm{<b>18</b>}}$,$\frac{9}{\mathrm{<b>18</b>}}$, $\frac{12}{\mathrm{<b>18</b>}}$ = $\frac{4}{9}$,$\frac{1}{2}$, $\frac{2}{3}$

Addition of fractions

Addition of Fractions with Same Denominators

To add fractions which have the same denominators, you simply add the numerators and divide by the denominator.

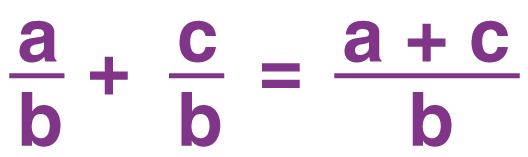
Example

$\frac{1}{2}$ + $\frac{3}{2}$ = $\frac{\mathrm{1+3}}{2}$ = $\frac{4}{2}$ = 2

Adding fractions with Different Denominators

To add fractions with different denominators, follow the steps below:

1. Write a division line below the fractions, place the least common factor of the denominators below that line (the numerator for the sum)

2. Multiply each of the numerators by the factor whose multiplication with the denominator gives the least common factor (L.C.M) placed under the division line and write the result on top of the division line.

3. Simplify the numerator.

4. Simplify the fraction if possible

Example

Add the fractions $\frac{4}{5}$ and $\frac{2}{3}$

Solution

Step 1

Denominators are 5 and 3

Multiples of 5 = {5 x 1 = 5, 5 x 2 = 10, 5 x 3 = 15, 5 x 4 = 20,...}
Multiples of 3 = {3 x 1 = 3, 3 x 2 = 6, 3 x 3 = 9, 3 x 4 = 12, 3 x 5 = 15, 3 x 6 = 18,...}

The least common multiple of 5 and 3 is 15

The numerator for the sum will be 15

Step 2

For the denominator, 5, it divides 15 exactly 3 times, hence we multiply its numerator (4) by 3

For the denominator, 3, it divides 15 exactly 5 times, hence we multiply its numerator (2) by 5

Step 3

Simplify the numerator and the resulting fraction.

$\frac{4}{5}$ + $\frac{2}{3}$

$\frac{\mathrm{4\; x\; <b>3</b>\; +\; 2\; x\; <b>5</b>}}{15}$

$\frac{\mathrm{12\; +\; 10}}{15}$

$\frac{22}{15}$ = 1 $\frac{7}{15}$

Addition of mixed fractions

To add mixed fractions, add the whole numbers separate and the fractions separate and put the results together.

Example 1

Add 2 $\frac{2}{5}$ and 1 $\frac{2}{3}$

Solution

Step 1

Add the whole number parts

2 + 1 = 3

Step 2

Add the fraction parts

Add $\frac{2}{5}$ + $\frac{2}{3}$ = $\frac{\mathrm{2\; x\; 3\; +\; 2\; x\; 5}}{15}$ = $\frac{\mathrm{6\; +\; 10}}{15}$ = $\frac{16}{15}$ = 1$\frac{1}{15}$

Put whole number and fraction parts together

3 + 1$\frac{1}{15}$ = 4 $\frac{1}{15}$

Example 2

Add 10 $\frac{2}{3}$ and 5 $\frac{1}{6}$

Solution

Step 1

Add the whole number parts

10 + 5 = 15

Add the fraction parts

$\frac{2}{3}$ + $\frac{1}{6}$ = $\frac{\mathrm{2\; x\; 2\; +\; 1\; x\; 1}}{6}$ = $\frac{\mathrm{4\; +\; 1}}{6}$ = = $\frac{5}{6}$

Put whole number and fraction parts together

15 + $\frac{1}{6}$ = 15 $\frac{5}{6}$

Alternatively, you can change the mixed fractions to improper fractions and add them

Examples 1

Add 7 $\frac{1}{2}$ and 5 $\frac{1}{4}$

Solution

7 $\frac{1}{2}$ = $\frac{\mathrm{2\; x\; 7\; +\; 1}}{2}$ = $\frac{\mathrm{14\; +\; 1}}{2}$ = $\frac{15}{2}$

5 $\frac{1}{4}$ = $\frac{\mathrm{4\; x\; 5\; +\; 1}}{4}$ = $\frac{\mathrm{20\; +\; 1}}{4}$ = $\frac{21}{4}$

7 $\frac{1}{2}$ + 5 $\frac{1}{4}$ = $\frac{15}{2}$ + $\frac{21}{4}$ = $\frac{\mathrm{2\; x\; 15\; +\; 1\; x\; 21}}{4}$ = $\frac{\mathrm{30\; +\; 21}}{4}$ = $\frac{51}{4}$ = 12 $\frac{3}{4}$

Examples 2

Add 2 $\frac{7}{8}$ and 3 $\frac{1}{3}$

Solution

2 $\frac{7}{8}$ = $\frac{\mathrm{2\; x\; 8\; +\; 7}}{8}$ = $\frac{\mathrm{16\; +\; 7}}{8}$ = $\frac{23}{8}$

3 $\frac{1}{3}$ = $\frac{\mathrm{3\; x\; 3\; +\; 1}}{3}$ = $\frac{\mathrm{9\; +\; 1}}{3}$ = $\frac{10}{3}$

2 $\frac{7}{8}$ + 3 $\frac{1}{3}$ = $\frac{23}{8}$ + $\frac{10}{3}$ = $\frac{\mathrm{3\; x\; 23\; +\; 8\; x\; 10}}{24}$ = $\frac{\mathrm{69\; +\; 80}}{24}$ = $\frac{149}{24}$ = 6 $\frac{5}{24}$

Adding fraction with whole number

To add whole number(s) with fractions, you can add the fractions and put the whole number and the fraction together to get a mixed fraction.

You can then change the mixed fraction to improper fraction.

Alternatively, you can change the whole number to fraction by dividing it by 1

Every number is divisible by 1 and the result is still the number.

Whole number to fraction = $\frac{\mathrm{Whole\; number}}{1}$

You can then add the fractions

Example 1

Add 2 and $\frac{1}{3}$

Method I

2 + $\frac{1}{3}$ = 2$\frac{1}{3}$ = $\frac{\mathrm{2\; x\; 3\; +\; 1}}{3}$ = $\frac{\mathrm{6\; +\; 1}}{3}$ = $\frac{7}{3}$

Method II

2 = $\frac{2}{1}$

2 + $\frac{1}{3}$ = $\frac{2}{1}$ + $\frac{1}{3}$ = $\frac{\mathrm{3\; x\; 2\; +\; 1}}{3}$ = $\frac{\mathrm{6\; +\; 1}}{3}$ = $\frac{7}{3}$

Note: The Least Common Multiples (L.C.M) of 1 and 3 is 3

The L.C.M of 1 and any number is the number.

Example 2

Add 2 and 3 $\frac{1}{3}$

Method I

2 + 3 $\frac{1}{3}$ = 2+3+$\frac{1}{3}$ = 5$\frac{1}{3}$ = $\frac{\mathrm{3\; x\; 5\; +\; 1}}{3}$ = $\frac{\mathrm{15\; +\; 1}}{3}$ = $\frac{16}{3}$

Method II

3 $\frac{1}{3}$ = $\frac{\mathrm{3\; x\; 3\; +\; 1}}{3}$ = $\frac{\mathrm{9\; +\; 1}}{3}$ = $\frac{10}{3}$

2 = $\frac{2}{1}$

2 + 3 $\frac{1}{3}$ = $\frac{2}{1}$ + $\frac{10}{3}$ = $\frac{\mathrm{3\; x\; 2\; +\; 1\; x\; 10}}{3}$ = $\frac{\mathrm{6\; +\; 10}}{3}$ = $\frac{16}{3}$

Subtraction of fraction

The method of subtraction is similar to addition. Instead of adding the numerators, they are subtracted.

Example 1

5 $\frac{3}{5}$ - 3 $\frac{1}{10}$

Method I

5 $\frac{3}{5}$ - 3 $\frac{1}{10}$ = (5-3)+ $\frac{3}{5}$ - $\frac{1}{10}$ = 2 + $\frac{\mathrm{2\; x\; 3\; -\; 1\; x\; 1}}{10}$ = 2 + $\frac{\mathrm{6\; -\; 1}}{10}$ = 2 + $\frac{5}{10}$ = 2 + $\frac{1}{2}$ = 2 $\frac{1}{2}$ or $\frac{5}{2}$

Method II

Change the mixed fractions to improper fractions and subtract

5 $\frac{3}{5}$ = $\frac{\mathrm{5\; x\; 5\; +\; 3}}{5}$ = $\frac{\mathrm{25\; +\; 3}}{5}$ = $\frac{28}{5}$

3 $\frac{1}{10}$ = $\frac{\mathrm{3\; x\; 10\; +\; 1}}{10}$ = $\frac{\mathrm{30\; +\; 1}}{10}$ = $\frac{31}{10}$

5 $\frac{3}{5}$ - 3 $\frac{1}{10}$ = $\frac{28}{5}$ - $\frac{31}{10}$ = $\frac{\mathrm{2\; x\; 28\; -\; 1\; x\; 31}}{10}$ = $\frac{\mathrm{56\; -\; 31}}{10}$ = $\frac{25}{10}$ = $\frac{5}{2}$

Multiplication of fraction by a number

When a whole number multiplies a fraction, the number multiplies the numerator and the denominator is maintained

In a situation where the denominator can divide the number multiplying, it can be simplified and the result multiplies the numerator.

Example 1

2 x $\frac{3}{5}$ = $\frac{\mathrm{2\; x\; 3}}{5}$ = $\frac{6}{5}$

Example 2

$\frac{3}{5}$ x 10 = 3 x 2 = 6

Note: 5 can divide 10, 2 times.

Multiplying a mixed fraction by a whole number

Method I

Multiply both the whole number part and the fraction part by the number

Method II

Change the mixed fraction to improper fraction before multiplying

Example 1

Method 1

4 x 8 $\frac{3}{5}$ = 4 x 8 + 4 x $\frac{3}{5}$ = 32 + $\frac{\mathrm{4\; x\; 3}}{5}$ = 32 + $\frac{12}{5}$ = 32 + 2$\frac{2}{5}$ = 34 $\frac{2}{5}$

Method II

8 $\frac{3}{5}$ = $\frac{\mathrm{8\; x\; 5\; +\; 3}}{5}$ = $\frac{\mathrm{40\; +\; 3}}{5}$ = $\frac{43}{5}$

4 x 8 $\frac{3}{5}$ = 4 x $\frac{43}{5}$ = $\frac{\mathrm{43\; x\; 4}}{5}$ = $\frac{172}{5}$ = 34 $\frac{2}{5}$

Multiplication of fraction by another fraction

During the multiplication of fraction, the numerators multiply each other and the denominators multiply each other

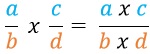
Note: If the fraction is mixed fraction, change it to improper fraction before multiplying.

Simplify the results by cancelling where possible.

Example 1

$\frac{2}{3}$ x $\frac{3}{5}$ = $\frac{\mathrm{2\; x\; 3}}{\mathrm{3\; x\; 5}}$ = $\frac{2}{5}$

NOTE: 3 cancels each other

Example 2

$\frac{3}{4}$ x 5 $\frac{1}{2}$

Change the mixed fraction to improper fraction.

5 $\frac{1}{2}$ = $\frac{\mathrm{2\; x\; 5\; +\; 1}}{2}$ = $\frac{\mathrm{10\; +\; 1}}{2}$ = $\frac{11}{2}$

$\frac{3}{4}$ x 5 $\frac{1}{2}$ = $\frac{3}{4}$ x $\frac{11}{2}$ = $\frac{\mathrm{3\; x\; 11}}{\mathrm{4\; x\; 2}}$ = $\frac{33}{8}$ = 4 $\frac{1}{8}$

Finding a fraction of a given quantity

In mathematics, of means multiplication

Example

In a class of 60 students, $\frac{2}{3}$ of the students speak Ga and $\frac{1}{3}$ speaks Twi.

How many students speak Ga and Twi?

Solution

Of means multiplication

$\frac{2}{3}$ of the students speak Ga

Students who speak Ga = $\frac{2}{3}$ x 60 = 2 x 20 = 40

Note: 3 divides 60 exactly 20 times

$\frac{1}{3}$ of the students speak Twi

Students who speak Twi = $\frac{1}{3}$ x 60 = 1 x 20 = 20

Division by a fraction

To divide a number or fraction by a fraction, multiply the number or fraction by the reciprocal of the fraction dividing.

Reciprocal means you switch the numerator and the denominator. Thus the denominator becomes the numerator and the numerator becomes the denominator

If mixed fraction(s) involved, change it to improper fraction before dividing.

Fraction being divided by another fraction

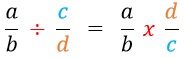
Whole number divided by a fraction

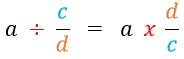
Every number is divisible by 1, the whole number can be expressed as a fraction by dividing it by 1.

Example 1

$\frac{3}{5}$ ÷ $\frac{4}{10}$ = $\frac{3}{5}$ x $\frac{10}{4}$ = $\frac{\mathrm{3\; x\; 10}}{\mathrm{5\; x\; 4}}$ = $\frac{\mathrm{3\; x\; 2}}{4}$ = $\frac{3}{2}$ = 1 $\frac{1}{2}$

Note: 5 cancels 10, 2 times and 2 also cancels 4, 2 times.

Example 2

2 $\frac{3}{4}$ ÷ $\frac{55}{24}$

2 $\frac{3}{4}$ = $\frac{\mathrm{4\; x\; 2\; +\; 3}}{4}$ = $\frac{\mathrm{8\; +\; 3}}{4}$ = $\frac{11}{4}$

2 $\frac{3}{4}$ ÷ $\frac{55}{24}$ = $\frac{11}{4}$ ÷ $\frac{55}{24}$ = $\frac{11}{4}$ x $\frac{24}{55}$ = $\frac{6}{5}$ = 1 $\frac{1}{5}$

Note: 11 cancels 55, 5 times and 4 cancels 24, 6 times.

Dividing a fraction by a number

When dividing a fraction by a number, change the number to fraction by dividing the number by 1 and divide the fraction by the new fraction.

Example 1

$\frac{1}{4}$ ÷ 8 = $\frac{1}{4}$ ÷ $\frac{8}{1}$ = $\frac{1}{4}$ x $\frac{1}{8}$ = $\frac{\mathrm{1\; x\; 1}}{\mathrm{4\; x\; 8}}$ = $\frac{1}{32}$

Example 2

$\frac{5}{6}$ ÷ 5 = $\frac{5}{6}$ ÷ $\frac{5}{1}$ = $\frac{5}{6}$ x $\frac{1}{5}$ = $\frac{\mathrm{5\; x\; 1}}{\mathrm{6\; x\; 5}}$ = $\frac{1}{6}$

NOTE: The 5 cancels each other.

Example 3

6 ÷ $\frac{1}{8}$ = $\frac{6}{1}$ x $\frac{8}{1}$ = $\frac{\mathrm{6\; x\; 8}}{\mathrm{1\; x\; 1}}$ = $\frac{48}{1}$ = 48

Fraction Formula

Fraction = $\frac{\mathrm{Part\; Value}}{\mathrm{Total\; Value}}$

Examples

There are 60 students in a class. 40 of the students speak Ga and 20 speak Twi.

What fraction of the student speak Ga and Twi?

Solution

Fraction = $\frac{\mathrm{Part\; Value}}{\mathrm{Total\; Value}}$

Total Value = 60

Part value for Ga = 40
Part value for Twi = 20

Ga Fraction = $\frac{40}{60}$ = $\frac{2}{3}$

Twi Fraction = $\frac{20}{60}$ = $\frac{1}{3}$

NOTE: The fraction for a whole part is 1/1. Thus if you sum all the fractions obtained from the group shared, you should get 1

For instance, in the above question, when we sum the fraction of students who speak Ga and Twi, it should give us 1

$\frac{2}{3}$ + $\frac{1}{3}$ = $\frac{\mathrm{2+1}}{3}$ = $\frac{3}{3}$ = 1

You could use this knowledge to calculate for a fraction when all other fractions are known by simply adding the other fractions and subtracting the result from 1

For instance, after we calculated that fraction of students who speak Ga, we could subtract it from 1 to get the fraction of students who speak Twi.

Students who speak Ga = $\frac{2}{3}$

Students who speak Twi = 1 - $\frac{2}{3}$

1 = $\frac{1}{1}$

Students who speak Twi = $\frac{1}{1}$ - $\frac{2}{3}$ = $\frac{\mathrm{3\; x\; 1\; -\; 1\; x\; 2}}{3}$ = $\frac{\mathrm{3\; -\; 2}}{3}$ = $\frac{1}{3}$

APPLICATION OF KNOWLEDGE

Question 1

The pie chart shows the monthly expenditure of Mr. Awuah whose monthly income is ₵18,000.00. Use the chart to answer the questions below.

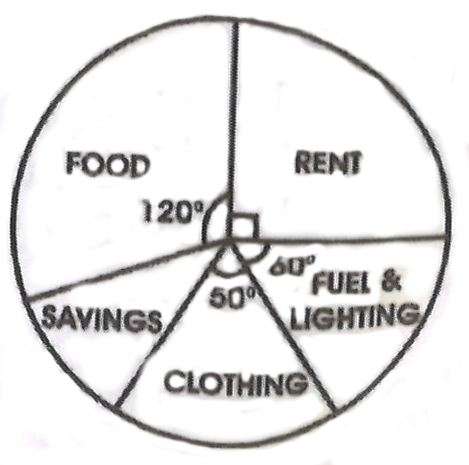
1. What fraction of Mr. Awuah's income is spent on food?

A. $\frac{1}{6}$ B. $\frac{1}{4}$ C. $\frac{1}{3}$ D. $\frac{2}{5}$

2. How much does Mr. Awuah spend on rent?

A. ₵9,000.00 B. ₵4,500.00 C. ₵90.00 D. ₵16,200.00

[B.E.C.E 1990 Section A Question 15 & 16]

NOTE: In a pie chart, the total angles is 360^o

The symbol for the angle for rent represents 90^o

Solution

Question 2

If $\frac{3}{15}$ is equivalent to $\frac{45}{\mathrm{<i>a</i>}}$, find a

A. 225 B. 150 C. 135 D. 30

[B.E.C.E 1990 Section A Question 22]

Solution

Question 3

Simplify 2 x(3$\frac{1}{3}$+1$\frac{1}{6}$)

A. 2$\frac{1}{3}$ B. 4$\frac{1}{2}$ C. 6$\frac{2}{3}$ D. 9

[B.E.C.E 1992 Section A Question 7]

NOTE: Simplify the fractions in the bracket first before multiplying the result by 2

The multiplication also affects everything in the bracket

Solution

Question 4

If 1:x is equivalent to 6$\frac{1}{4}$ : 25, find x

A. 4 B. 6.25 C. 24 D. 100

[B.E.C.E 1992 Section A Question 35]

NOTE: A fraction could also be written as a proportion. Thus you can express a proportion representation as a fraction.

a : b = $\frac{\mathrm{<i>a</i>}}{\mathrm{<i>b</i>}}$

Solution

Question 5

Express $\frac{3}{8}$ as a percentage.

A. 0.375% B. 12$\frac{1}{2}$% C. 25% D. 37$\frac{1}{2}$%

[B.E.C.E 1992 Section A Question 36]

Solution

Question 6

Arrange the fraction $\frac{3}{4}$, $\frac{2}{3}$, $\frac{3}{5}$ in ascending order.

A. $\frac{2}{3}$, $\frac{3}{4}$, $\frac{3}{5}$ B. $\frac{3}{4}$, $\frac{2}{3}$, $\frac{3}{5}$ C. $\frac{3}{5}$, $\frac{2}{3}$, $\frac{3}{4}$ D. $\frac{3}{5}$, $\frac{3}{4}$, $\frac{2}{3}$

[B.E.C.E 1993 Section A Question 7]

Solution

Question 7

Which of the following inequality is/are true?

I: $\frac{5}{6}$ > $\frac{3}{4}$ II: $\frac{3}{4}$ < $\frac{3}{5}$ III: $\frac{3}{8}$ > $\frac{1}{2}$

A. I only B. II only C. III only D. I and II only

[B.E.C.E 1993 Section A Question 11]

Solution

Question 8

Simplify (3$\frac{1}{2}$ + 7)÷(4$\frac{1}{3}$ - 3)

A. 6$\frac{7}{8}$ B. 7 C. 7$\frac{7}{8}$ D. 10$\frac{1}{2}$

[B.E.C.E 1993 Section A Question 23]

Solution

Question 9

Evaluate ($\frac{2}{3}$ - $\frac{1}{4}$) ÷ $\frac{5}{6}$.

A. $\frac{1}{2}$ B. $\frac{1}{5}$ C. $\frac{5}{12}$ D. $\frac{25}{72}$

[B.E.C.E 1994 Section A Question 27]

Solution

Question 10

Divide (1$\frac{1}{2}$ + $\frac{1}{4}$) by (1$\frac{1}{2}$ - $\frac{1}{4}$)

A. $\frac{5}{7}$ B. 1 C. 1$\frac{2}{5}$ D. 1$\frac{3}{4}$

[B.E.C.E 1995 Section A Question 6]

Solution

Question 11

Arrange the following fractions in descending order.

$\frac{3}{4}$,$\frac{5}{8}$,$\frac{4}{5}$,$\frac{13}{20}$

A. $\frac{4}{5}$,$\frac{3}{4}$,$\frac{13}{20}$,$\frac{5}{8}$ B. $\frac{4}{5}$,$\frac{5}{8}$,$\frac{3}{4}$,$\frac{13}{20}$ C. $\frac{5}{8}$,$\frac{4}{5}$,$\frac{3}{4}$,$\frac{13}{20}$ D. $\frac{3}{4}$,$\frac{5}{8}$,$\frac{4}{5}$,$\frac{13}{20}$

[B.E.C.E 1995 Section A Question 22]

Solution

Question 12

Simplify $\frac{1}{3}$ - $\frac{1}{2}$ + $\frac{2}{5}$

A. $\frac{17}{30}$ B. $\frac{13}{30}$ C. $\frac{7}{30}$ D. -$\frac{7}{30}$

[B.E.C.E 1996 Section A Question 9]

Solution

Question 13

Which of the following fractions is the greatest?

$\frac{1}{6}$,$\frac{1}{4}$,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{5}$

A. $\frac{1}{6}$ B. $\frac{1}{2}$ C. $\frac{1}{4}$ D. $\frac{1}{3}$

[B.E.C.E 1999 Section A Question 14]

Solution

Question 14

Kwame travelled from Accra to Kumasi. He travelled $\frac{3}{10}$ of the journey by lorry $\frac{2}{10}$ of the journey by taxi and the rest by train. What fraction of the journey did he travel by train?

A. $\frac{1}{2}$ B. $\frac{3}{5}$ C. $\frac{7}{10}$ D. $\frac{3}{25}$

[B.E.C.E 1999 Section A Question 28]

Solution

Question 15

Simplify $\frac{2}{3}$ of 6$\frac{3}{4}$÷(2$\frac{4}{15}$ - 1$\frac{2}{3}$).

[B.E.C.E 2000 Section B Question 1 (a)]

NOTE: Apply BODMAS, which is the order to follow to simplify mathematical expressions.

B = Brackets
O = Orders (Powers/indices/roots)
D = Division
M = Multiplication
A = Addition
S = Subtraction

Solution

Question 16

By how much is $\frac{5}{6}$ greater than $\frac{3}{4}$?

A. $\frac{1}{12}$ B. $\frac{1}{6}$ C. $\frac{5}{12}$ D. $\frac{2}{3}$

[B.E.C.E 2001 Section A Question 8]

Solution